GAMES101

发表于 更新于 分类于 阅读次数：
本文字数： 7.7k 阅读时长 ≈ 39 分钟
GAMES101:现代计算机图形学入门

Lecture1: intro

计算机图形学

使用计算机synthesize(合成) manipulate（操作) 可视化信息

why study computer graphics?

  • Application
    • video games 电子游戏
    • animations 动画
    • visualization 可视化
    • virtual reality
    • augmented reality 增强现实
    • digital illustration 数码插画
    • simulation 模拟
    • graphical user interfaces 图形用户界面
    • typography 排版
  • technical chanllenges

Course topics

  • Rasterization 光栅化

    • project geometry primitives (3D triangles / polygons) onto the screen

      将几何图形（3D三角形 / 多边形）投射到屏幕上

    • break projected primitives into fragments (pixels)

      将投影图元分解到片段(像素)

    • gold standard in video games (real-time applications)

  • curves and meshes 曲线和栅格

    • 怎样represent geometry in CG

  • ray tracing 光线追踪

    • shoot rays from camera though each pixel
      • calculate intersection and shading 交叉点和阴影
      • continue to bounce the rays till they hit light sources
    • gold standard in animations / movies (offline离线 application)

  • animation simulation

    • key frame animation 关键帧动画
    • mass-spring system 弹簧振子系统

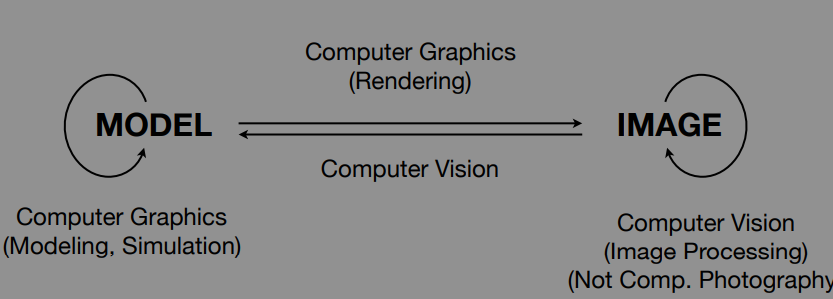
differences between cg and cv

No clear boundaries

image-20210913210044004

Lecture2: review of linear algebra

Graphics’ dependcies

  • basic mathematics
    • Linear algebra 线性代数
      • mostly dependent on linear algebra
      • vectors（dot products点乘,cross products叉乘
        • An operation like translating or rotating objects can be matrix-vector multiplication
      • matrices 矩阵（复数
    • calculus 微积分
    • statistics 统计
  • basic physics
    • Optics, 光学的
    • Mechanics 机械的
  • misc 杂项
    • Numerical analysis 数值分析
    • signal processing 信号处理
    • aesthetics 审美

vectors

noting: 只记了part

  • unit vector

    • 单位向量，
    • 用来代表方向

  • dot product in graphics

    • $\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}|cos\theta$

    • Find angle between two vectors (e.g. cosine of angle between light source 光源 and surface表面)

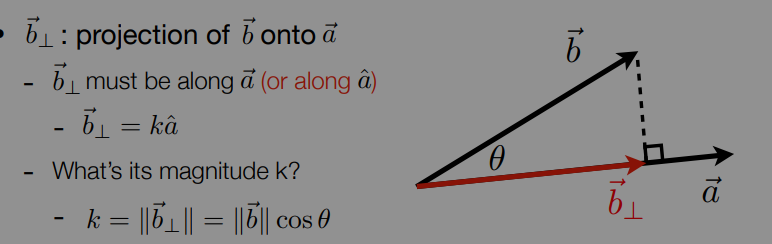
    • image-20210913215253056

    • Finding projection of one vector on another

      • measure how close two directions are

      • decompose分解 a vector

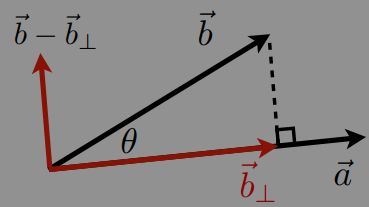
        image-20210913215715680

      • determine forward or backward

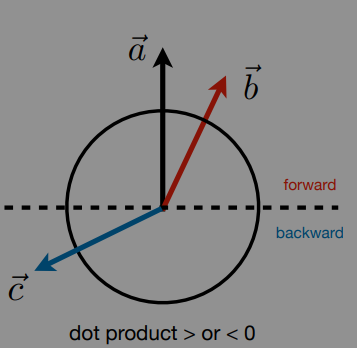
        image-20210913215758162

  • cross product in graphics

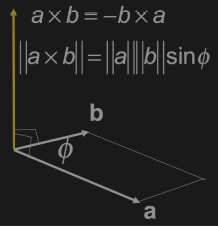
    ​ image-20210913220439863

    • Direction determined by right-hand rule

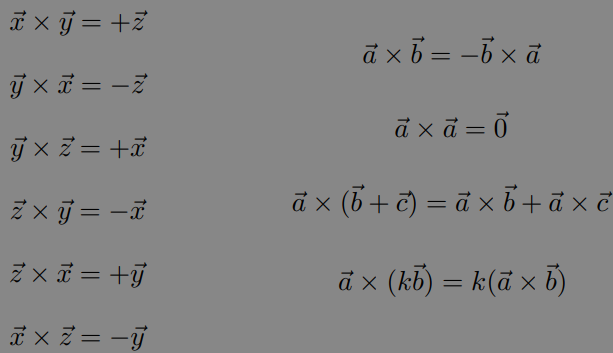
  • image-20210913220739158

    • Useful in constructing coordinate systems (later)
    • Determine left / right
    • Determine inside / outside
  • Orthonormal bases and coordinate frames 正交基底和坐标系
    • Critical issue is transforming between these systems/ bases

matrices

image-20210913223344462

  • $(AB)^{T} = B^{T}A^{T}$
  • $AA^{-1} = A^{-1}A = I$
  • $(AB)^{-1} = B^{-1}A^{-1}$

image-20210913223854494

In Graphics, pervasively used to represent transformations

  • translation, rotation,shear剪切,scale缩放

Lecture 3: Transformation

why study transformation

  • modeling
    • translation
    • rotation
    • scaling
  • viewing
    • 3D (projection)
    • 2D (projection)

2D transformations:

  • representing transformations using matrices

  • rotation

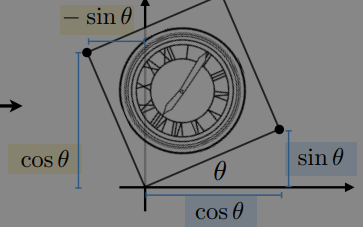
    image-20210914135044036

    • $R_{\theta} = \begin{bmatrix} cos\theta & -sin\theta \ sin\theta & cos\theta \end{bmatrix} $
    • $R{-\theta} = \begin{bmatrix} cos\theta & sin\theta \ -sin\theta & cos\theta \end{bmatrix} = R{\theta}^{T} = R_{\theta}^{-1}(by \quad definition) $
    • 正交矩阵： A·A^T^ = E
    • 默认绕原点旋转
    • 默认逆时针旋转

  • scale matrix

    $\begin{bmatrix} x^{‘} \ y^{‘} \end{bmatrix} = \begin{bmatrix} s{x} & 0 \ 0 & s{y} \end{bmatrix}\begin{bmatrix} x \ y \end{bmatrix}$

  • reflection matrix 反射（镜像）矩阵

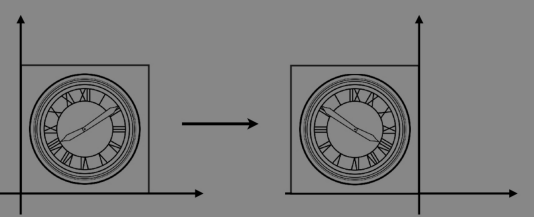
    image-20210914124142211

    $\begin{bmatrix} x^{‘} \ y^{‘} \end{bmatrix} = \begin{bmatrix} -1 & 0 \ 0 & 1\end{bmatrix}\begin{bmatrix} x \ y \end{bmatrix}$

  • shear matrix

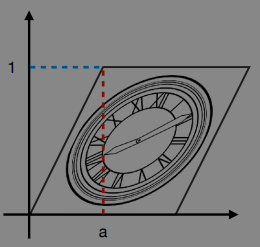
    ​ image-20210914134632720

    $\begin{bmatrix} x^{‘} \ y^{‘} \end{bmatrix} = \begin{bmatrix} -1 & a \ 0 & 1\end{bmatrix}\begin{bmatrix} x \ y \end{bmatrix}$

    • Hints:
      • horizontal shift is 0 at y = 0
      • horizontal shift is a at y = 1
      • vertical shift is always

  • Linear transforms

    • 线性变换：可以用一个矩阵表示的变换
    • x’ = ax + by
    • y’ = cx + dy
    • $\begin{bmatrix} x^{‘} \ y^{‘} \end{bmatrix} = \begin{bmatrix} a & b \ c & d \end{bmatrix}\begin{bmatrix} x \ y \end{bmatrix}$

Homogeneous coordinates 齐次坐标

  • Why homogeneous coordinates

    for example: translation

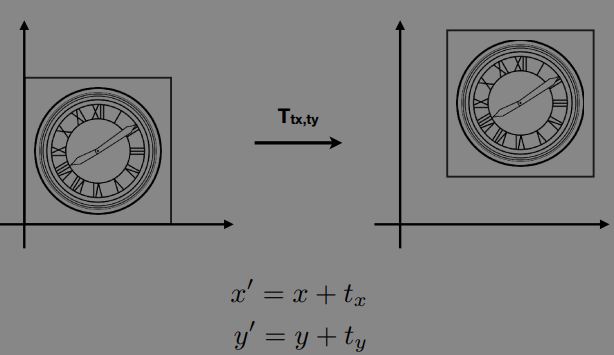
    image-20210914135548707

    $\begin{bmatrix} x^{‘} \ y^{‘} \end{bmatrix} = \begin{bmatrix} a & b \ c & d \end{bmatrix}\begin{bmatrix} x \ y \end{bmatrix} + \begin{bmatrix} t{x} \ t{y} \end{bmatrix} $

    • so, translation is not linear transform!

    • 因为平移变换不能直接用一个矩阵表示，必须加一个向量；

    • add a third coordinates

      引入齐次坐标可以解决问题，让平移也能只用一个矩阵表示

    • 2D point = (x,y,1)^T^

    • 2D vector = (x,y,0)^T^

    • 向量 + 向量，结果齐次项是0，还是向量

    • 点 - 点，得到的是一个向量，齐次项也变成0

    • 点 + 向量，表示一个点的移动，结果 还是点 ！

    • 点 + 点是什么呢？齐次项变成2。将所有项除以2，齐次项又变为1 。所以点 + 点结果实际上是两个点的中点。

  • Affine transformation 仿射变换

    • 仿射变换：先线性变换再加上一次平移

    • $\begin{bmatrix} x^{‘} \ y^{‘} \ 1 \end{bmatrix} = \begin{bmatrix} a & b & t{x}\ c & d & t{y} \ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \ y \ 1 \end{bmatrix} $

    • scale

      $ S(s{x}, s{y}) = \begin{bmatrix} s{x} & 0 & 0 \ 0 & s{y} & 0 \ 0 & 0 & 1 \end{bmatrix}$

    • rotation

      $ R(\alpha) = \begin{bmatrix} cos\alpha & -sin\alpha & 0 \ sin\alpha & cos\alpha & 0 \ 0 & 0 & 1 \end{bmatrix}$

    • translation

      $ T(t{x}, t{y}) = \begin{bmatrix} 1 & 0 & t{x} \ 0 & 1 & t{y} \ 0 & 0 & 1 \end{bmatrix}$

  • transform ordering matters

    • matrix multiplication is not commutative 可交换的

composing transforms

  • decomposing complex transforms

    • translate center to origin
    • rotate
    • translate back

    image-20210914142248083

    which means $T(c) · R(\alpha) · T(-c)$

    • 分解：变换可以分解，注意先后顺序是从右到左

    • 2D变换矩阵（缩放，旋转，平移变换）

Lecture 4： Transformation Cont

3D transformations

  • 3D point = (x,y,z,1)^T^

  • 3D vector = (x,y,z,0)^T^

  • $\begin{bmatrix} x^{‘} \ y^{‘} \ z{‘} \ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & t{x}\ d & e & f & t{y}\g & h & i & t{z} \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \ y \z \ 1 \end{bmatrix} $

  • 三维空间中的齐次变换，最后一行和二维变换类似，是0 0 0 1，平移还是在矩阵最后一列

  • 对于仿射变换，是先应用线性变换，再加上平移

  • what is order?

    • linear transform first or translation first?

    • scale

      $S(s{x}, s{y},s{z}) = \begin{bmatrix} s{x} & 0 & 0 & 0\ 0 & s{y} & 0 & 0\0 & 0 & s{z} & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} $

    • translation

      $T(t{x}, t{y}, t{z}) = \begin{bmatrix} 1 & 0 & 0 & t{x}\ 0 & 1 & 0 & t{y} \0 & 0 & 1 & t{z} \ 0 & 0 & 0 & 1 \end{bmatrix} $

    • rolation

      • rolation around x-, y-,or z-axis

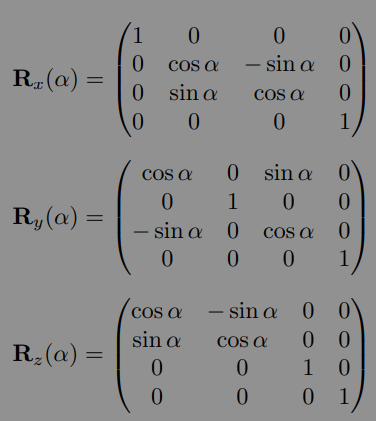
      image-20210914203043532

      • 绕哪个轴旋转，哪个坐标就不变

      • 不过𝑅𝑦矩阵稍微不同，其他两个都是右上角𝑠𝑖𝑛是负的，只有他是左下角𝑠𝑖𝑛是负的 因为𝑥叉乘𝑦得到𝑧，𝑧叉乘𝑦得到𝑥，但是𝑧叉乘𝑥得到𝑦（而不是𝑥叉乘𝑧），所以是反的

      • $R{xyz}(\alpha, \beta, \gamma) = R{x}(\alpha)R{y}(\beta)R{z}(\gamma)$

    • image-20210914220208915

Viewing (观测) transformation

  • View (视图) / Camera transformation

    • Think about how to take a photo
      • Find a good place and arrange people (model transformation)
      • Find a good “angle” to put the camera (view transformation)
      • Cheese! (projection transformation)
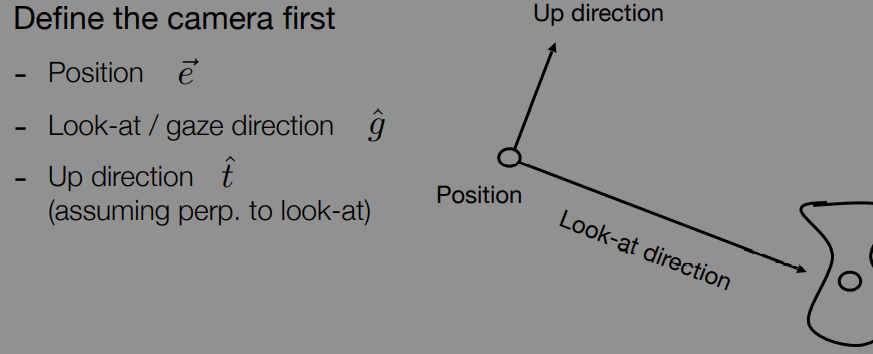
        • image-20210914224154439
        • 定义相机
        • 位置
        • 往哪看
        • 向上方向
        • 现实中是移动相机，变换景物
        • 图形学中，相机不动，永远在原点
        • image-20210914223829896
        • 经过变换，把相机的位置移动到原点，同时保持看到的景物不变

  • image-20210914225726865

  • 这个从“歪”的坐标轴旋转回正的坐标轴，不太好写。 但是这个变换的逆过程，即：从正的坐标轴旋转到“歪”的坐标轴，是好写的， 于是我们先写从“正”坐标轴变换到“歪”坐标轴的变换矩阵，再求其逆矩阵，就可以得到待求的变换矩阵。 又因为旋转矩阵是正交矩阵，所以他的逆矩阵就只需要转置一下就可以得到了！ 注意，不但相机要做这个变换，其他物体也要做这个变换，因为我们想让相机看到的景物相对不变。 （以上部分个人认为非常巧妙和关键！）

  • Projection (投影) transformation

    • 3D to 2D

    • Orthographic (正交) projection

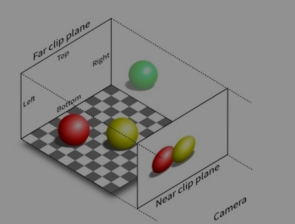
      image-20210914230821994

      • 没有近大远小
      • 平行投影
        • 首先定义空间中一个立方体，将其translate，使其中心在原点，再scale成标准立方体（边长为2
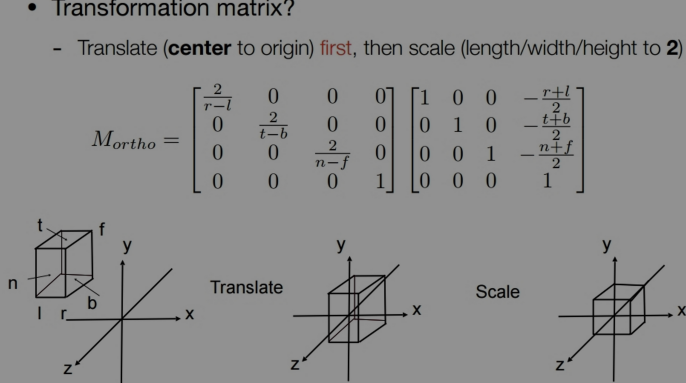
      • image-20210915120758604
      • 再次提醒，注意𝑧轴是近大远小 OpenGL等API是反过来的

    • Perspective (透视) projection

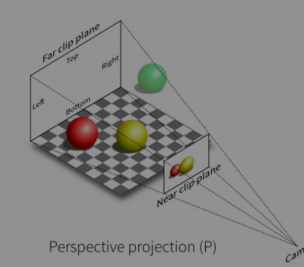
      image-20210914230840011

      • 更像人眼看到的场景

      • Most common in Computer Graphics, art, visual system

      • Further objects are smaller

      • Parallel lines not parallel; converge to single point

      • Recall: property of homogeneous coordinates
        • (x, y, z, 1), (kx, ky, kz, k != 0), (xz, yz, z2, z != 0) all represent the same point (x, y, z) in 3D
        • e.g. (1, 0, 0, 1) and (2, 0, 0, 2) both represent (1, 0, 0)
      • how to do perspective projection
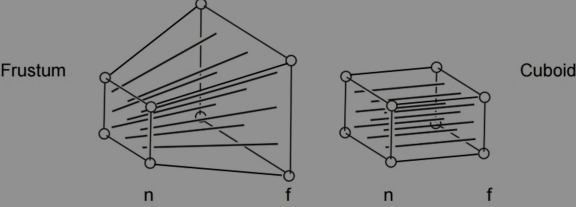
        • image-20210915122816233
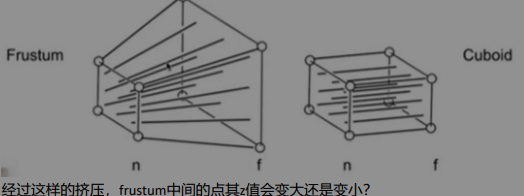
        • 先将frustum远平面，挤压成和近平面一样大（从左图变成右图）
        • 再做正交投影，投影到近平面
        • 上述操作过程中几点假设：
          • 1）近平面保持不变
          • 2）z值保持不变，只是向内收缩
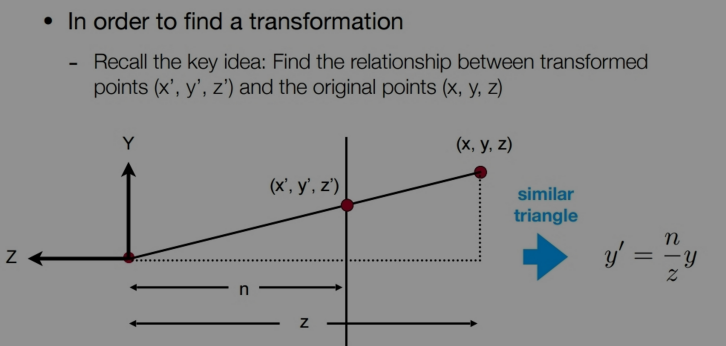
      • image-20210915122907760
      • image-20210915122956833
      • 挤压这一步怎么做？ 上图是从侧面观察frustum 用相似三角形知识可以得到新坐标的表达式，但是第三个分量目前还不知道（这里利用之前讲的那个性质： 齐次坐标，如果我们对点的坐标所有分量同时乘以k，他表示的还是原来那个点！
      • image-20210915123123207
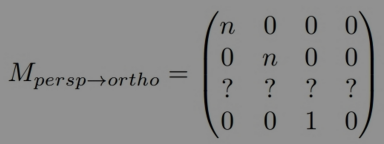
      • image-20210915123140120
      • 如何求解第三行
        • 任何近平面上的点不会改变（也就是对于任意的(𝑥, 𝑦, 𝑛, 1)，经过这个矩阵变换后，点的位置仍然不变）
        • 任何远平面上的点，𝑧值不会改变
        • image-20210915123415483
        • 点(𝑥, 𝑦, 𝑧, 1)是可以通过矩阵变换得到(𝑛𝑥, 𝑛𝑦, 𝑢𝑛𝑘𝑛𝑤𝑜𝑛, 𝑧)向量的。 根据上文提到的性质（1），经过这个变换，点实际没有改变 而同时，(𝑥, 𝑦, 𝑧, 1)本身可以写成(𝑥, 𝑦, 𝑛, 1)（为什么把𝑧替换成𝑛？因为近平面的𝑧坐标就是都是𝑛，所以可以做这个替换。）然后同时乘以𝑛， 变成(𝑛𝑥, 𝑛𝑦, 𝑛 ଶ , 𝑛) 经过上面两个推导，可以看出，第三行前两个数一定是0 因为𝑛 ଶ这个分量和𝑥和𝑦都毫无关系，因此前两个数必定是0 这样，我们就解出了第三行前两个数，都是0 接下来求A和B
        • image-20210915123459854
        • 远平面上有一个特殊点，(0, 0, 𝑓)经过变换挤压仍然不变 所以(0, 0, 𝑓)经过变换仍然是(0, 0, 𝑓) 根据近平面我们得到$An + B = n^{2}$,根据远平面的中心点我们得到$Af + B = f^{2}
        • image-20210915123625508
        • 这样我们就能解出A和B了， 这样终于把从透视投影挤压成正交投影的矩阵，解出来了
        • image-20210915123651566

    • 思考题

      • image-20210915123709902

Lecture05: Rasterization 1(Triangles)

Finishing up Viewing

  • Viewport(视口) transformation

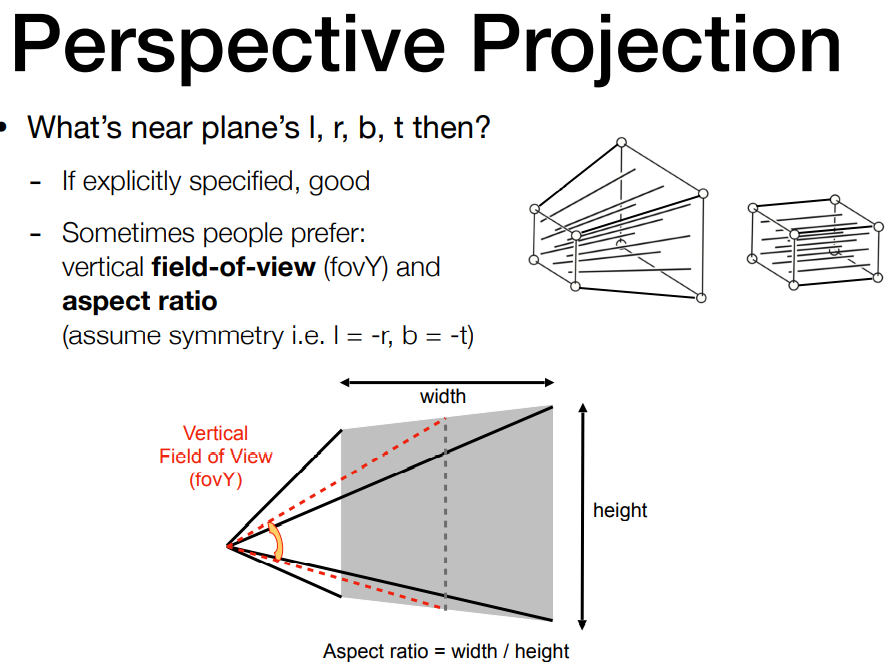
image-20211005190731847

上节课把透视投影转化成正交投影 这里引入另外一个概念 Field of View，表示你能看到的角度的范围 注意看上图中红色线的夹角，就是垂直可视角度，他越大，可视角度越大 同理还有水平可视角度

image-20211005190926969

MVP这三个变换之后，所有东西都会停留在一个1，1，1的位于原点的标准立方体中 下一步就要把这立方体画在屏幕上

Rasterization（光栅化，即把东西花在屏幕上

屏幕

  • 像素是最小的屏幕单位

  • 每个像素有不同的颜色

  • 屏幕空间：就是给屏幕定义一个坐标系 比如，可以定义左下角是原点。

  • 实际上像素的中心是(𝑥 + 0.5, 𝑦 + 0.5)

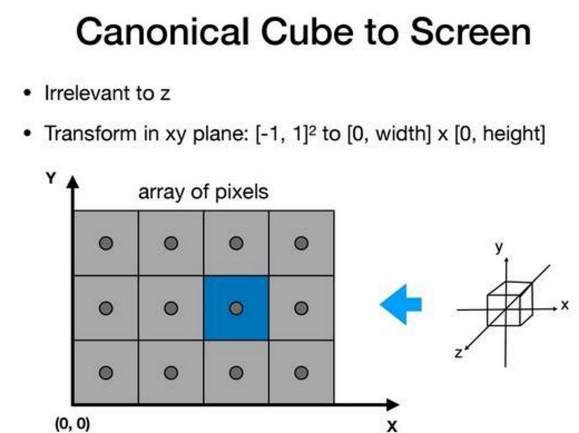
  • image-20211005191523440

  • image-20211005191556944

    我们要做的就是把标准立方体空间映射到屏幕这个二维世界中去 𝑧暂时不管 其他两个坐标是[−1, 1] ଶ转换到 [0, 𝑤𝑖𝑑𝑡ℎ] ∗ [0, ℎ𝑒𝑖𝑔ℎ𝑡] 使用上面这个矩阵做变换

Rasterizing a triangle

  • 三角形可以拼接在三维空间中的面，或者二维空间中复杂的图形

    image-20211005191718242

  • 三角形内部一定是平面的

  • 给三角形顶点定义不同属性，可以在三角形内部进行插值
  • 通过采样的方式，来画出三角形
    • 采样就是把函数离散化的过程
    • 可以对时间，面积，方向，体积… 进行采样

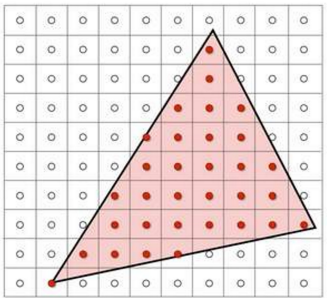
image-20211005191941468

定义二值函数：

  • 这里我们要做的就是给定一个三角形，判断像素中心是否在三角形内部。

    image-20211005192820679

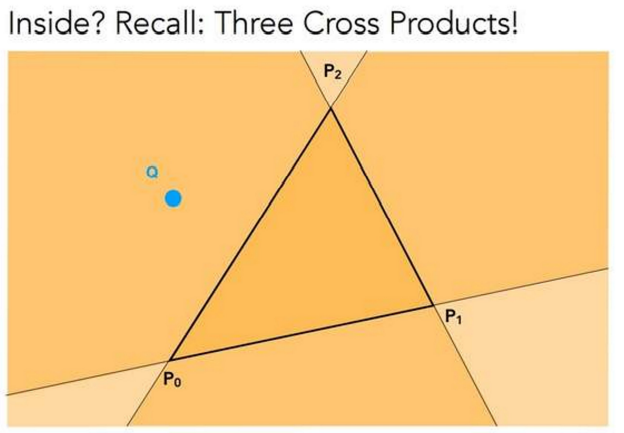
image-20211005192920137

那么，如何判断一个点是否在三角形内？用叉乘！！ 比如对上图，判断Q是否在三角形内部 首先$𝑃1𝑃2 \ X \ 𝑃1𝑄 $，将会得到一个z为正数的向量，也就是结果向量朝向屏幕外的，利 用右手定则，可以得知𝑄在𝑃1𝑃2的左侧（因为如果在右侧，那么结果将会是向量𝑧为负 数，那么结果向量就朝向屏幕内部） 类似的𝑃2𝑃0 𝑋 𝑃2𝑄，得到𝑄在右侧，不对劲！ 𝑃0𝑃1 𝑋 𝑃0𝑄，得到𝑄在左侧

注意，向量按照一定的顺序去判断，比如我们上面是按照P1, P2, P0去判断的

image-20211005193137111

检查屏幕所有的像素太花时间！ 可以只检查蓝色的包围盒（Bounding box）部分

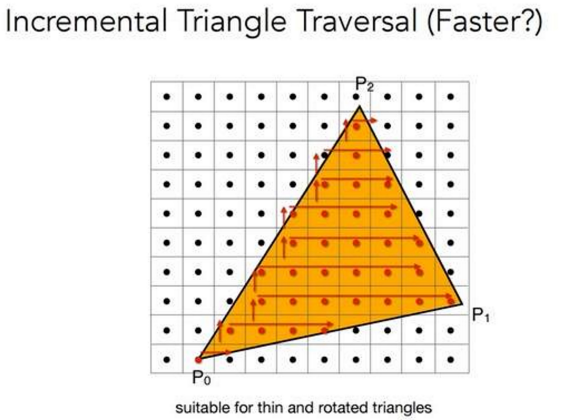
image-20211005193213667

也可以每一行设置一个包围盒，进一步减小包围盒 很适用于那种三角形很小，但是包围盒很大的（窄长三角形