matlab学习笔记

注：

• 虽然文档很全面，但是这篇文章主要是为了在一天内速成，所以不足之处请多包涵。
• 代码基于vscode/py 3.6调用的matlab terminal

基本的数学运算与矩阵运算

基本语法

变量

• 不需声明
• 用 = 给变量赋值

变量名

• 变量名大小写敏感（不知道是不是因为在windows的原因
• 变量名只能由[0~9,a~z,A~z,_]组成,且变量名不能以数字开头.
• 保留变量不适合做变量名
  • 使用iskeyword命令可以查看程序关键字,这些关键字不允许被用作变量名.

变量	意义
ans	上一句运算的结果
i,j	复数算子，（这里需要留意）
Inf	无穷
eps	浮点相对精度,即1.0到下一个浮点数之间的距离(值为2.2204e-16)
NaN	非数字
pi	圆周率

• 变量名不应当覆盖内置函数名

  • 在MATLAB中,变量的调用优先级(calling priority)高于函数,因此变量名不应该覆盖内置函数.

    

  • 例如：

    cos = 'changqingaas';
    cos(8)
    % disp(['ans is ', num2str(ans)])
    clear; % 若某函数被变量名所覆盖,则调用clear <变量名>可以取消绑定在该函数名上的变量名
    cos(8)
    % disp(['ans is ', num2str(ans)])

    注：clear是一个比较危险的命令,因为该命令后若不加参数,则表示清除当前工作区内的所有变量.

输出：

ans =

    'n'


ans =

   -0.1455

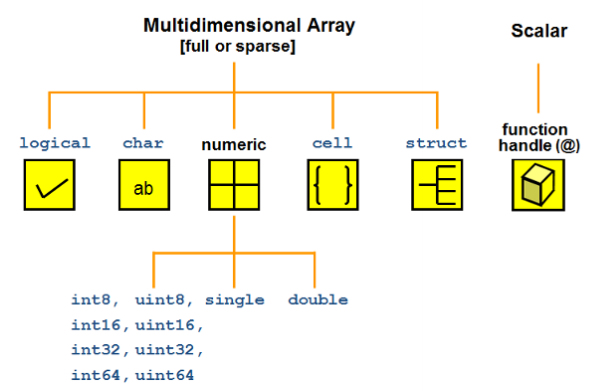
变量类型

logical,char,numeric,cell,struct以及由他们组成的数组或矩阵.

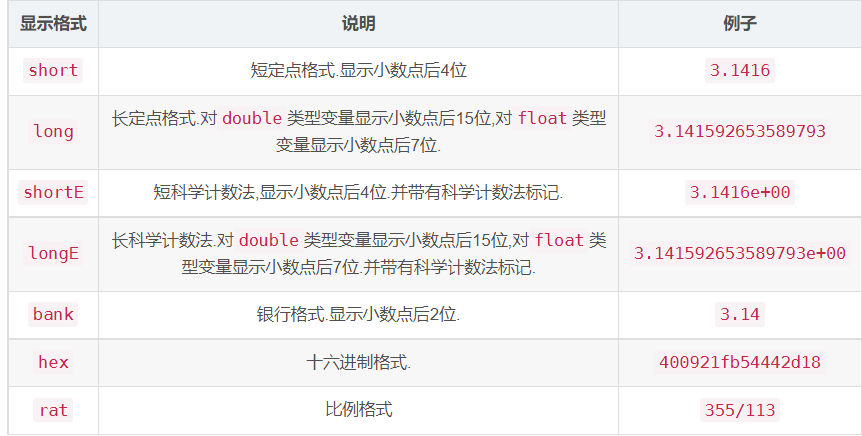
数字型变量的显示格式

数字型变量,默认以double形式存储的.

可以通过format <显示格式>改变数字型变量的显示格式.

MATLAB命令行

• 使用行尾;抑制输出:

  • 在一行命令后使用;抑制输出,否则运算结果将被显示在终端上.

• | 命令 | 作用 | 运行结果 |
  | ———- | —————————————————————————————— | —————————————————————————————— |
  | clc | 清除终端的输出 | |
  | clear | 默认清除当前工作区内所有变量 | |
  | who | 以简略格式显示工作区内所有变量 | 您的变量为:
  ans |
  | whos | 以复杂格式显示工作区内所有变量 | Name Size Bytes Class Attributes
  ans 1x1 8 double |
  | which | 查看内置函数源代码文件的位置,与edit命令结合可以查看内置函数的源代码. | |

使用MATLAB进行数字运算

使用MATLAB计算数学表达式

• 数学表达式被计算后，其值被存入变量ans
• log 表示 ln
• exp(x) 表示 e^x

MATLAB内置的数学函数

• MATLAB内置的算数运算函数

  • 基本运算:

    • 加: +,sum,cumsum,movsum
    • 减: -,diff
    • 乘: .*,*,prod,cumprod
    • 除: ./,.\,/,\
    • 乘方: .^,^

  • 取模运算: mod,rem,idivide,ceil,fix,floor,round

• MATLAB内置的三角运算函数

  • 正弦: sin,sind,sinpi,asin,asind,sinh,asinh
  • 余弦: cos,cosd,cospi,acos,acosd,cosh,acosh
  • 正切: tan,tand,atan,atand,atan2,atan2d,tanh,atanh
  • 余割: csc,cscd,acsc,acscd,csch,acsch
  • 正割: sec,secd,asec,asecd,sech,asech
  • 余切: cot,cotd,acot,acotd,coth,acoth
  • 斜边: hypot
  • 转换: deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart

• MATLAB内置的指数对数函数:

  • exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqr

• MATLAB内置的复函数:

  • abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap

使用MATLAB进行矩阵运算

定义矩阵

向终端输入矩阵

在MATLAB中,使用[]将待输入的矩阵内容括起来,使用空格或逗号,分隔行内变量,使用;分隔每一行.

MATLAB命令	得到的矩阵
[1 2 3 4]	[1 2 3 4]
[1; 2; 3; 4]	$\begin{bmatrix}1 \ 2 \ 3 \ 4\end{bmatrix}$
[1 21 6; 5 17 9; 31 2 7]	$\begin{bmatrix} 1 & 21 & 6 \ 5 & 17 & 9 \ 31 & 2 & 7 \end{bmatrix}$

使用冒号运算符创建向量

使用冒号运算符:可以创建一个长向量,其语法如下:

冒号表达式	得到的结果
j:k	[j,j+1,j+2,…,k]
j:i:k	[j,j+i,j+2*i,…,j+m∗i]

例如：

MATLAB语句	得到的结果
1:5	[1 2 3 4 5]
1:3:5	[1 4]
[1:3; 2:3:10]	$\begin{bmatrix} 1 & 2 & 3 \ 2 & 5 & 8 \end{bmatrix}$
‘a’:2:’z’	‘acegikmoqsuwy’

定义特殊矩阵

命令	得到的结果
eye(n)	得到一个n × n 的单位矩阵
zeros(n1, n2)	得到一个n1 × n2 的全0矩阵
ones(n1, n2)	得到一个n1 × n2 的全1矩阵
diag(vector)	得到一个以向量vector中内容为对角线的对角矩阵

矩阵的索引

• MATLAB中的矩阵是以列序存储的.且索引下标从1开始.

• 矩阵有两种索引方式: 按一维索引和按二维索引.对于一个一般的矩阵,其索引顺序如下:

  • $\begin{bmatrix} 1或(1,1) & 4或(1,2) & 7或(1,3) \ 2或(2,1) & 5或(2,2) & 8或(2,3) \ 3或(3,1) & 6或(3,2) &9或(3,3) \end{bmatrix}$

• 矩阵的索引可以使用冒号:,表示选取所有行或所有列.

• 矩阵的索引可以是一个或两个向量,表示选中向量内的所有行或所有列.

  | 原矩阵 | 索引 | 得到的结果 |
  | —————————————————————————————— | ———————- | ———————————————————————————- |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A(8) | 6 |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A([1 3 5]) | [1 7 5] |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A([1 2; 3 4]) | $\begin{bmatrix} 1 & 4 \ 7 & 2\end{bmatrix}$ |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A(3,2) | 8 |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A([1,2], :) | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{bmatrix}$ |
  | $\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}$ | A([1 3], [1 2]) | $\begin{bmatrix} 1 & 2 \ 7 & 8 \end{bmatrix}$ |

矩阵的操作

操作矩阵的运算符

运算符	操作	形式	例子
+	矩阵与向量相加	A+b	[6 3] + 2 = [8 5]
-	矩阵与向量相减	A-b	[6 3] - 2 = [4 1]
+	矩阵与矩阵对应位置相加	A+B	[6 3] + [4 8] = [10 11]
-	矩阵与矩阵对应位置相减	A-B	[6 3] - [4 8] = [2 -5]
*	矩阵与矩阵相乘	A*B	[6 3] * [4 8]' = 48
.*	矩阵与矩阵对应位置相乘	A.*B	[6 3] * [4 8] = [24 24]
/	矩阵与矩阵右除(等价于A*inv(B))	A/B	[6 3] / [4 8] = 0.6
\	矩阵与矩阵左除(等价于inv(A)*B)	A\B	[6 3] / [4 8] = [0.06667 1.3333; 0 0]
./	矩阵与矩阵对应位置右除	A./B	[6 3] ./ [4 8] = [1.5 0.375]
.\	矩阵与矩阵对应位置左除	A.\B	[6 3] .\ [4 8] = [0.6667 2.6667]
^	矩阵与向量乘方	A^b	[1 2; 3 4]^3 = [37 54; 81 118]
.^	矩阵与矩阵对应位置乘方	A.^B	[1 2; 3 4].^[1 2; 3 4] = [1 4; 27 256]

操作矩阵的函数

对下面的矩阵

$$A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 0 & 9 \end{bmatrix}$$

进行操作以演示操作矩阵的常见函数

函数	作用	例子	结果
max(A, [], dim)	获取矩阵A的dim维度上的最大值	max(A, [], 1)	$\begin{bmatrix} 7 & 5 & 9 \end{bmatrix}$
min(A, [], dim)	获取矩阵A的dim维度上的最小值	min(A, [], 2)	$\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}$
sum(A, dim)	获取矩阵A的dim维度上的和	sum(A, 1)	$\begin{bmatrix} 8 & 7 & 18 \end{bmatrix}$
mean(A, dim)	获取矩阵A的dim维度上的平均值	mean(A, 1)	[2.66672.33336.0000]
sort(A, dim, direction)	获取矩阵A的dim维度上按direction顺序排序结果	sort(A, 1, 'descend')	$\begin{bmatrix} 7 & 5 & 9 \\ 1 & 2 & 6 \ 0 & 0 & 3 \end{bmatrix}$
sortrows(A, column)	获取矩阵A按照每行第column个元素升序排序结果.	sortrows(A, 2)	$\begin{bmatrix} 7 & 0 & 9\ 1 & 2 & 3\ 0 & 5 & 6\end{bmatrix}$
size(A, dim)	获取矩阵A的dim维度上的形状.若不指定dim,则返回整个矩阵的形状.	size(A)	[3 3]
find(A, n)	获取矩阵A前n个非零元素的索引	`find(A,5)	[1 3 4 5 7]

对于上面这些函数,除第一个参数以外,其它参数都是可选的.

结构化编程和函数定义

结构化编程

流程控制语句和逻辑运算符

流程控制语句	作用
if, elseif, else	若if语句为真,则执行子句
switch, case, otherwise	根据switch语句内容判断执行哪个子句
while	重复执行子句直到while中的条件为假
for	执行子句固定次数
try, catch	执行子句并捕获执行过程中的异常
break	跳出循环
continue	直接进入下一次循环
end	结束子句
pause	暂停程序
return	返回到调用函数处

上述所有循环和条件语句都要在末尾以end闭合.

MATLAB还有以下逻辑运算符:

运算符	意义
==	等于
~=	不等于
&&	且(支持逻辑短路)
`		`	或(支持逻辑短路)

流程控制语句示例

if 语句：

if condition1
	statement1
elseif condition2
	statement2
else 
	statement3
end

switch语句

switch expression
    case value1
        statement1
    case value2
        statement2
    otherwise 
        statement
end

while语句

while expression
	statement
end

for语句

for variable = start:increment:end
	commands
end

break语句

x = 2; k = 0; error = inf;
error_threshold = 1e-32;

while error > error_threshold

    if k > 100
        break
    end

    x = x - sin(x) / cos(x);
    error = abs(x - pi);
    k = k + 1;
end

使用循环语句应尽量预先分配内存空间

编写脚本时应注意的问题

在脚本开头应添加语句清空工作区

在每个脚本的开头,应添加下述语句,清空工作区缓存以及之前程序运行的痕迹:

clear all	% 清空工作区内存中的变量
close all 	% 关闭之前程序绘制的图像
clc			% 清空之前程序在终端的输出

在运算和赋值语句后应添加分号;抑制输出

在所有运算和赋值语句都应该添加分号;抑制输出,若需要向终端输出一个变量,应对其调用disp方法.

使用省略号...拼接多行语句

在MATLAB中,省略号...可以将多行语句拼接为一行,灵活使用该语句可以提高代码可读性.

函数

与脚本类似,函数可以被存入函数名.m文件中,也可以以函数句柄的形式定义在内存中.

查看内置函数

我们可以使用which命令查看内置函数源代码文件的位置,与edit命令结合可以查看内置函数的源代码.

运行下面语句可以打开MATLAB内置的mean函数的源文件:

edit(which('mean.m'))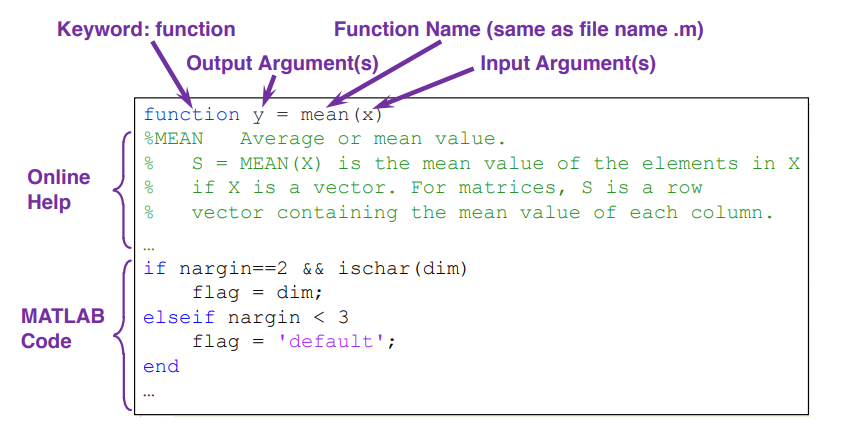

以函数名.m文件形式定义函数

在MATLAB文件中定义函数的格式如下:

function [输出变量名] = 函数名(输入变量名) 
% 函数的文档

函数代码

• function是一个关键字,声明该文件中保存的是一个函数.
• 输入变量和输出变量是非必须的,函数既可以没有输入变量,也可以没有输出变量.
• 函数名应与.m文件名相同,且不包含特殊字符(最好不要有中文).

MATLAB内置的函数参数

函数参数	意义
imputname	输入变量名列表
mfilename	函数源代码文件名
nargin	输入变量数
nargout	输出变量个数
varargin	可变长输入参数列表
varargout	可变长输出参数列表

MATLAB不提供其他高级语言的指定默认参数值以及函数重载等语法,但灵活使用上述内置的函数参数,可以在一定程度上实现指定默认参数值以及方法重载:

MATLAB函数定义示例1

面程序用来计算自由落体运动中位移量:
$x = x{0} + v{0}t + \frac{1}{2} g t^2 $

function x = freebody(x0,v0,t)
% calculation of free falling
% x0: initial displacement in m
% v0: initial velocity in m/sec
% t: the elapsed time in sec
% x: the depth of falling in m
x = x0 + v0.*t + 1/2*9.8*t.*t;

该函数演示了一个MATLAB编程技巧: 计算乘法时应尽量使用.*而非*,因为前者不仅对参数t为标量的情况可用,也对变量t为向量或矩阵的情况可用.

freebody(0, 0, 2)			% 得到 19.6000
freebody(0, 0, [0 1 2 3])	% 得到 [0 4.9000 19.6000 44.1000]
freebody(0, 0, [0 1; 2 3])	% 得到 [0 4.9000; 19.6000 44.1000]

MATLAB函数定义示例2

下面函数实现了从华氏温度到摄氏温度的转换,该函数可以识别输入的待转换样例的个数,当输入的待转换样例个数为0时,退出函数.

function F2C()
while 1
    F_degree = input('tempreature in Fahrenheit: ', 's');
    F_degree = str2num(F_degree);
    if isempty(F_degree)
        return
    end
    C_degree = (F_degree-32)*5/9;
    disp(['tempreature in Celsius: ' num2str(C_degree)])
end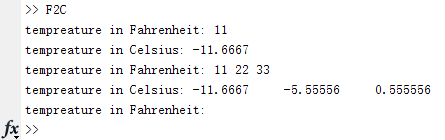

以函数句柄形式定义函数

我们也可以使用函数句柄的形式定义函数,这更接近数学上的函数定义,其语法如下:

函数句柄 = @(输入变量) 输出变量 

可以直接通过函数句柄调用该方法.

f = @(x) exp(-2*x);
x = 0:0.1:2;
plot(x, f(x));

数据类型与文件读写

数据类型

MATLAB中主要的数据类型如下:

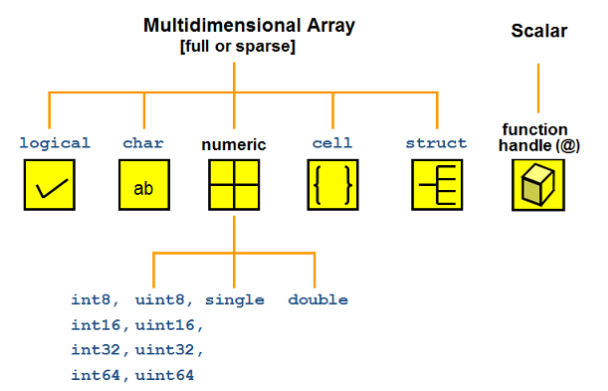
数值类型(numeric)

MATLAB支持的数值类型见下表:

数值类型	描述
double	双精度浮点数
single	单精度浮点数
int8	8位带符号整数
int16	16位带符号整数
int32	32位带符号整数
int64	64位带符号整数
uint8	8位无符号整数
uint16	16位无符号整数
uint32	32位无符号整数
uint64	64位无符号整数

在MATLAB中,数值类型的变量被默认为double类型的,可以使用类型转换将其转换为其他数值类型.

n = 3;
class(n)	 

n = int8(3);
class(n)	 

输出：

ans =
    'double'
ans =
    'int8'

字符串类型(char)

• 在MATLAB中,字符串类型由一对单引号'包裹一段文字来定义.标准ASCII字符可以被转换为对应的ASCII码.

  s1 = 'h';
  uint16(s1)	% 得到 104

• 字符串在内存中是以字符矩阵的形式存储的,可以对其进行矩阵的索引以及赋值操作:

  str1 = 'hello';
  str2 = 'world';
  
  str3 = [str1 str2];
  size(str3)		% 得到 [1 10]
  
  str4 = [str1; str2];
  size(str4)		% 得到 [2 5]

  str = 'aardvark';
  'a' == str				% 得到 [1 1 0 0 0 1 0 0]
  str(str == 'a') = 'Z'	% 得到 'ZZrdvZrk'

结构体(structure)

在MATLAB中,结构体是一个键值对

结构体的基本使用

• 与大多数编程语言类似,MATLAB使用.来访问结构体中的字段:

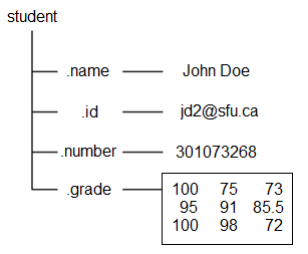
student.name = 'John Doe';
student.id = 'jdo2@sfu.ca';
student.number = 301073268;
student.grade = [100, 75, 73; ...
                 95, 91, 85.5; ...
                 100, 98, 72];
student

• 对结构体列表使用下标表达式可以扩充或缩减结构体列表.

  

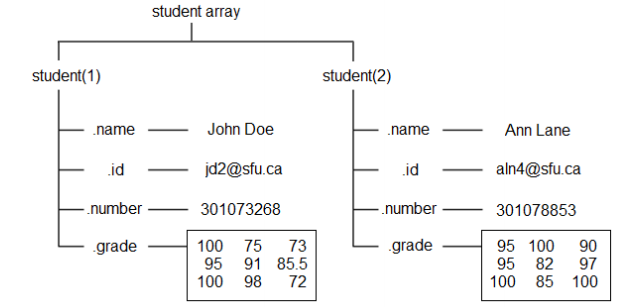
  student.name = 'John Doe';
  student.id = 'jdo2@sfu.ca';
  student.number = 301073268;
  student.grade = [100, 75, 73; 95, 91, 85.5; 100, 98, 72];
  
  student
  
  student(2).name = 'Ann Lane';
  student(2).id = 'aln4@sfu.ca';
  student(2).number = 301078853;
  student(2).grade = [95 100 90; 95 82 97; 100 85 100];
  
  student(1) = [] % 删除student列表第一项

• 结构体可以级联,即结构体中字段的取值也可以是结构体:

  A = struct('data', [3 4 7; 8 0 1], ...
  'nest', struct('testnum', 'Test 1', ...
  'xdata', [4 2 8], ...
  'ydata', [7 1 6]));
  A(2).data = [9 3 2; 7 6 5];
  A(2).nest.testnum = 'Test 2';
  A(2).nest.xdata = [3 4 2];
  A(2).nest.ydata = [5 0 9];
  
  A

结构体的常用函数

函数	作用
struct	创建结构体
struct2cell	将结构体转换为元胞数组
cell2struct	将元胞数组转换为结构体
isstruct	判断某变量是否是结构体
structfun	对结构体的每个字段都应用某函数
fieldnames	获取结构体的所有字段名
isfield	判断结构体是否包含某字段
getfield	获取结构体某字段的值
setfield	为结构体中的某字段赋值
rmfield	删除结构体中的某字段
orderfields	为结构体字段排序

元胞数组(cell)

在MATLAB中,元胞数组是一个可以容纳不同类型元素的数据结构,类似于Python语言中的列表.

元胞数组的基本使用

• 使用{}像定义矩阵一样定义元胞数组: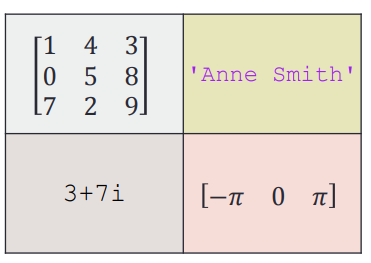

  

  A = { [1 4 3; 0 5 8; 7 2 9]		'Anne Smith' ;...
  3+7i		-pi:pi:pi}

A(1,1)={[1 4 3; 0 5 8; 7 2 9]};
A(1,2)={'Anne Smith'};
A(2,1)={3+7i};
A(2,2)={-pi:pi:pi};

A{1,1}=[1 4 3; 0 5 8; 7 2 9];
A{1,2}='Anne Smith';
A{2,1}=3+7i;
A{2,2}=-pi:pi:pi;
A

上面三种方式是等价的,其中第二种方式使用单元索引赋值,而第三种方式使用内容索引赋值.

• 有两种方式访问元胞数组中的数据,分别是: 单元索引()和内容索引{}

  因为元胞数组的子集仍为元胞数组,在索引器内容的使用,我们有必要指明我们要访问的的是一个子元胞数组还是元胞数组对应区域中的内容.

  • 使用单元索引(),我们得到的是一个子元胞数组.

    • 使用内容索引{},我们得到的是元胞数组对应区域中的内容.

元胞数组的常用函数

元胞数组的常用函数

函数	作用
cell	创建一个元胞数组
iscell	判断某变量是否为元胞数组
cell2mat	将元胞数组转为矩阵
cell2struct	将元胞数组转为结构体
mat2cell	将数组转换为指定大小元胞数组
num2cell	将数组转换为相同大小的元胞数组
struct2cell	将结构体转换为元胞数组
celldisp	递归显示元胞数组中的内容
cellplot	以图像形式绘制元胞数组的结构
cellfun	对元胞数组的每个元胞应用某函数

其中mat2cell函数可以在转换的时候指定元胞数组各元胞的尺寸.

a = magic(3)

b = num2cell(a)
% 得到
% [8] [1] [6]
% [3] [5] [7]
% [4] [9] [2]

c = mat2cell(a, [1 2], [2, 1])
% 得到
% [1x2 double] [6]
% [2x2 double] [2x1 double]

高维元胞数组

一个三维的元胞数组可以有行(row),列(column),层(layer)三个维度.在对元胞数组进行索引时,优先级从高到低的顺序分别是: 行→列→层.

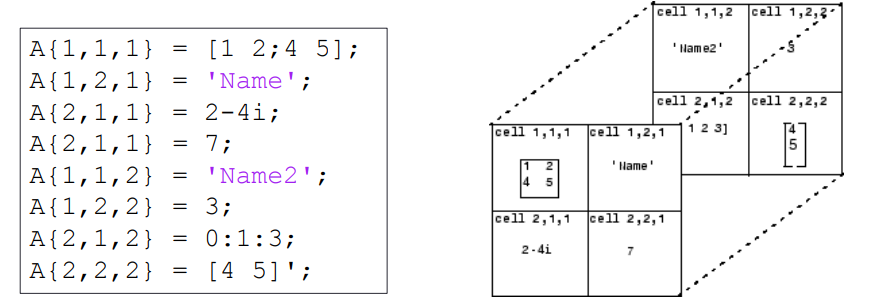
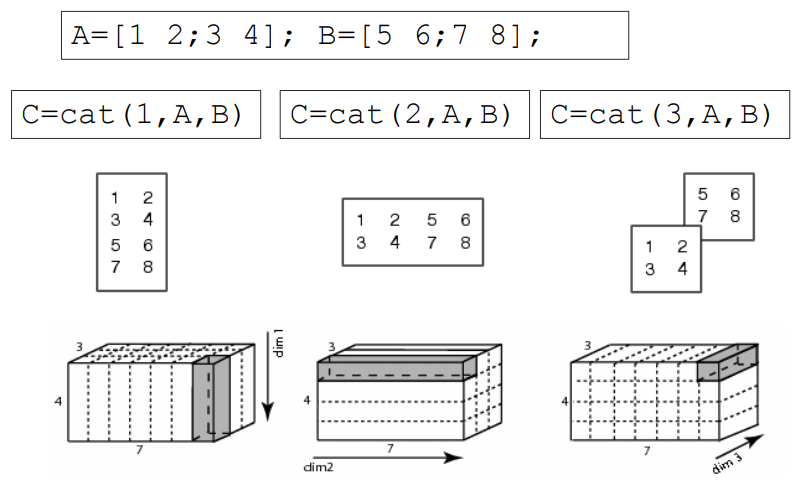
使用cat函数可以在指定维度上对元胞数组进行拼接.

判断变量数据类型的函数

下列函数可以对变量类型进行判断:

函数	作用
isinteger	判断输入参数是否为整型数数组
islogical	判断输入参数是否为逻辑量数组
isnumeric	判断输入参数是否为数值数组
isreal	判断输入参数是否为实数数组
ischar	判断输入参数是否为字符数组
iscell	判断输入参数是否为元胞数组
isfloat	判断输入数组是否为浮点数组
ishandle	判断输入数组是否有效的图形句柄
isempty	判断输入数组是否为空
isprime	确定哪些数组元素为质数
isnan	确定哪些数组元素为NaN
isinf	确定哪些数组元素为Inf
isequal	判断数组是否相等

文件读写

支持的文件类型如下:

文件内容	扩展名	读取文件的函数	写入文件的函数
MATLAB数据	*.mat	load	save
Excel表格	*.xls,*.xlsx	xlsread	xlswrite
空格分隔的数字	*.txt	load	save

读写MATLAB格式的数据

MATLAB工作区内的数据可以以*.mat格式保存在文件中.使用save函数将数据存入文件,使用load函数从文件中读取数据.

• save

  函数的语法如下:

  • save(filename,variables)将变量variables以二进制形式存入文件中.
  • save(filename,variables,'-ascii')将变量variables以文本形式存入文件中.

• load

  函数的语法如下:

  • load(filename)从二进制形式文件中读取数据.
  • load(filename,'-ascii')从文本形式文件中读取数据.

其中参数filename和variables都是字符串格式,若不指定variables参数,则将当前工作区内所有变量存入文件中.

复杂的数据格式,如struct和cell,不支持以二进制格式存储.

读写Excel表格

使用xlsread和xlswrite函数可以读写Excel数据,语法如下:

• 读取Excel文件的语法:[num,txt,raw] = xlsread(filename,sheet,xlRange)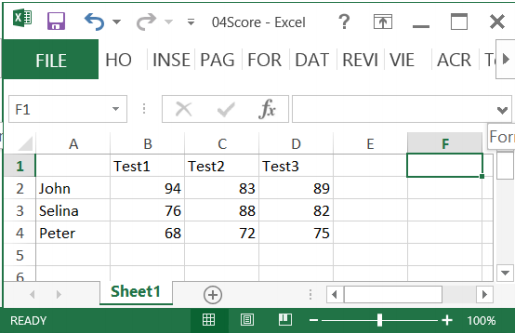

  

  Score = xlsread('04Score.xlsx')
  Score = xlsread('04Score.xlsx', 'B2:D4')
  [Score Header] = xlsread('04Score.xlsx')

• 写入Excel的语法:xlswrite(filename,A,sheet,xlRange)

  M = mean(Score);
  xlswrite('04Score.xlsx', M, 1, 'E2:E4');
  xlswrite('04Score.xlsx', {'Mean'}, 1, 'E1');

基础绘图

图线的绘制与装饰

使用plot()函数绘制图线

在MATLAB中,使用plot()函数绘制图线,其语法为:

plot(x,y,LineSpec)

LineSpec: 图线的线条设定,三个指定线型,标记符号和颜色的设定符组成一个字符串,设定符不区分先后.具体细节请参考官方文档.

线型符号	线型设定符	标记	标记设定符	颜色	颜色设定符
-	实线（默认）	o	圆圈	y	黄色
--	虚线	+	加号	m	品红色
:	点线	*	星号	c	青蓝色
-.	点划线	.	点	r	红色
		x	叉号	g	绿色
		s	方形	b	蓝色
		d	菱形	w	白色
		^	上三角	k	黑色
		v	下三角
		>	右三角
		<	左三角
		p	五角形
		h	六角形

注：Python中的matplotlib的画图方式和这里几乎一样

装饰图线

• 使用legend()函数为图片增加图例

  使用legend(label1, ..., labelN)函数可以为图片添加图例.

  x=0:0.5:4*pi;
  y=sin(x); h=cos(x); w=1./(1+exp(-x)); g=(1/(2*pi*2)^0.5).*exp((-1.*(x-2*pi).^2)./(2*2^2));
  plot(x,y,'bd-' ,x,h,'gp:',x,w,'ro-' ,x,g,'c^-');		% 绘制多条图线
  legend('sin(x)','cos(x)','Sigmoid','Gauss function');	% 添加图例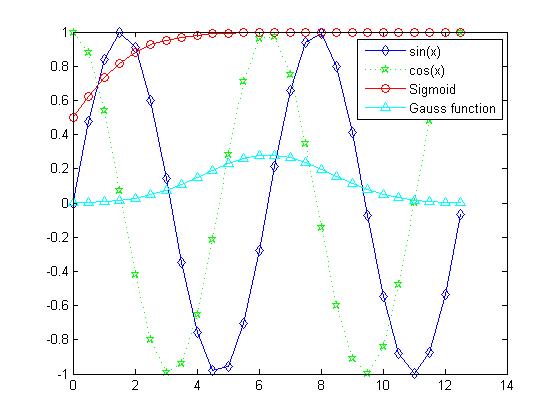

  

• 使用title()和*label()为图片增加标题和标签

  x = 0:0.1:2*pi; y1 = sin(x); y2 = exp(-x);
  plot(x, y1, '--*', x, y2, ':o');
  xlabel('t = 0 to 2\pi');
  ylabel('values of sin(t) and e^{-x}')
  title('Function Plots of sin(t) and e^{-x}');
  legend('sin(t)','e^{-x}');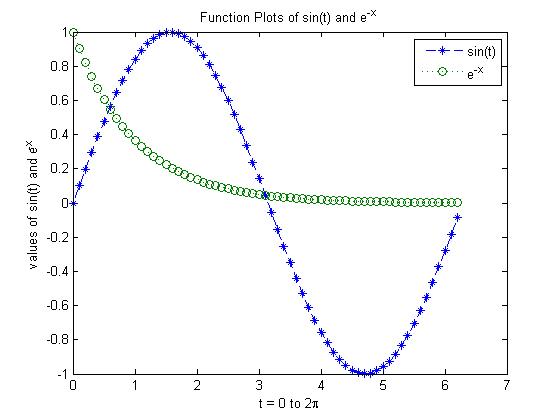

  

• 使用text()和annotation()为图片增加注解

  x = linspace(0,3); y = x.^2.*sin(x); plot(x,y);
  line([2,2],[0,2^2*sin(2)]);
  str = '$$ \int_{0}^{2} x^2\sin(x) dx $$';
  text(0.25,2.5,str,'Interpreter','latex');
  annotation('arrow','X',[0.32,0.5],'Y',[0.6,0.4]);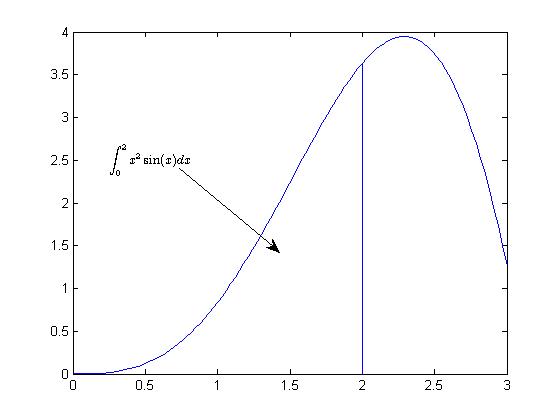 

  

控制坐标轴,边框与网格

命令	作用
grid on/off	设置网格可见性
box on/off	设置边框可见性
axis on/off	设置坐标轴可见性
axis normal	还原默认行为,将图框纵横比模式和数据纵横比模式的属性设置为自动
axis square	使用相同长度的坐标轴线,相应调整数据单位之间的增量
axis equal	沿每个坐标轴使用相同的数据单位长度
axis tight	将坐标轴范围设置为等同于数据范围,使轴框紧密围绕数据

下面的例子演示axis命令的效果:

t = 0:0.1:2*pi; x = 3*cos(t); y = sin(t);
subplot(2, 2, 1); plot(x, y); axis normal
subplot(2, 2, 2); plot(x, y); axis square
subplot(2, 2, 3); plot(x, y); axis equal
subplot(2, 2, 4); plot(x, y); axis equal tight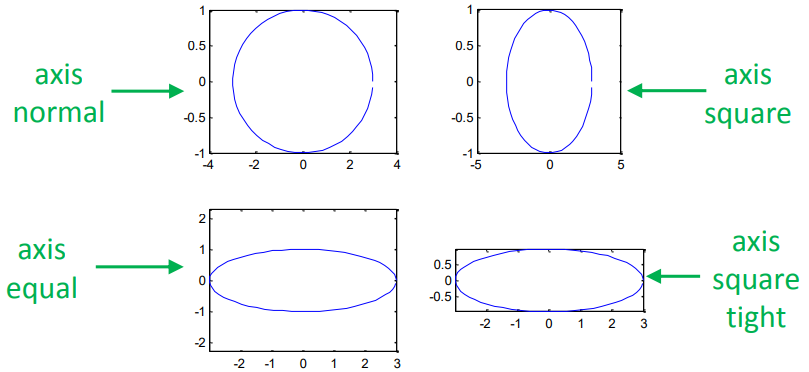

绘制多条图线

在一个图像上绘制多条图线

默认情况下,每次执行plot()函数都会清除上一次绘图的结果,多次执行plot()只会保留最后一次绘制的图形.

我们可以使用hold on和hold off命令控制绘图区域的刷新,使得多个绘图结果同时保留在绘图区域中.

hold on		% 提起画笔,开始绘制一组图片			
plot(cos(0:pi/20:2*pi));
plot(sin(0:pi/20:2*pi));
hold off	% 放下画笔,该组图片绘制完毕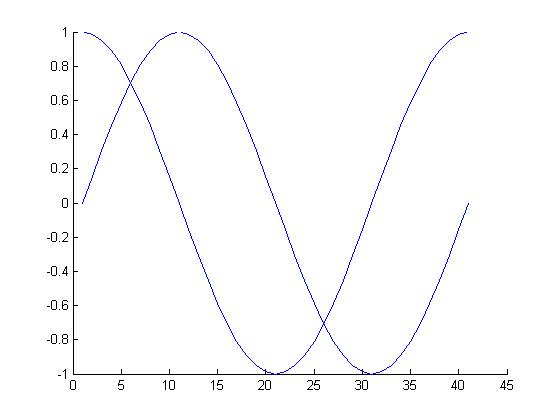

在一个窗口内绘制多个图像

subplot

图形对象的操作

在MATLAB中,图形都是以对象的形式储存在内存中,通过获取其图形句柄可以对其进行操作.

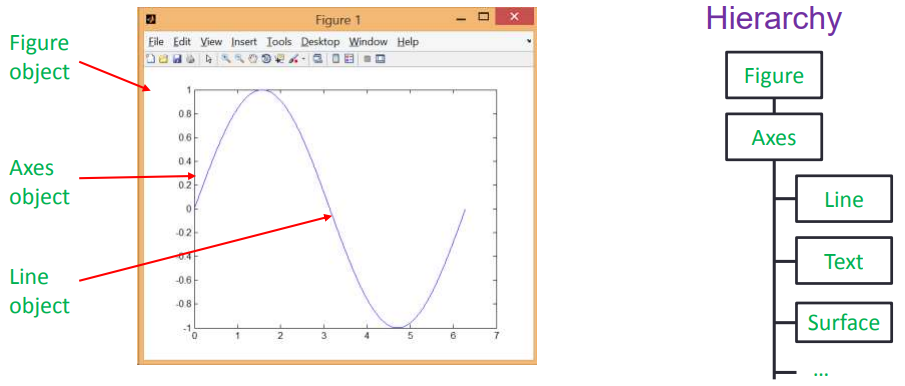
获取图形句柄

图形句柄本质上就是一个浮点数,可以唯一确定一个图形对象.下面几个函数用于获取图形句柄.

Function	Purpose
gca()	获取当前坐标轴的句柄
gcf()	获取当前图像的句柄
allchild(handle_list)	获取该对象的所有子对象的句柄
ancestor(h,type)	获取对象最近的type类型的祖先节点
delete(h)	删除某对象
findall(handle_list)	获取该对象的后代对象

所有绘图函数也会返回图形对象的句柄.

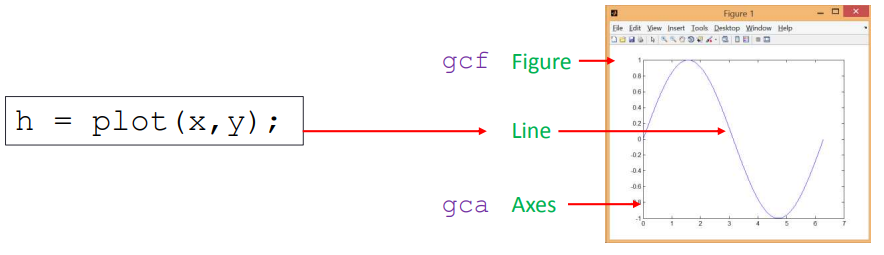
通过图形句柄操作图形属性

使用get()和set()函数可以对图形对象的属性进行访问和修改.访问官方文档可以查看所有图形对象的属性.

• set(H,Name,Value)

• v = get(h,propertyName)

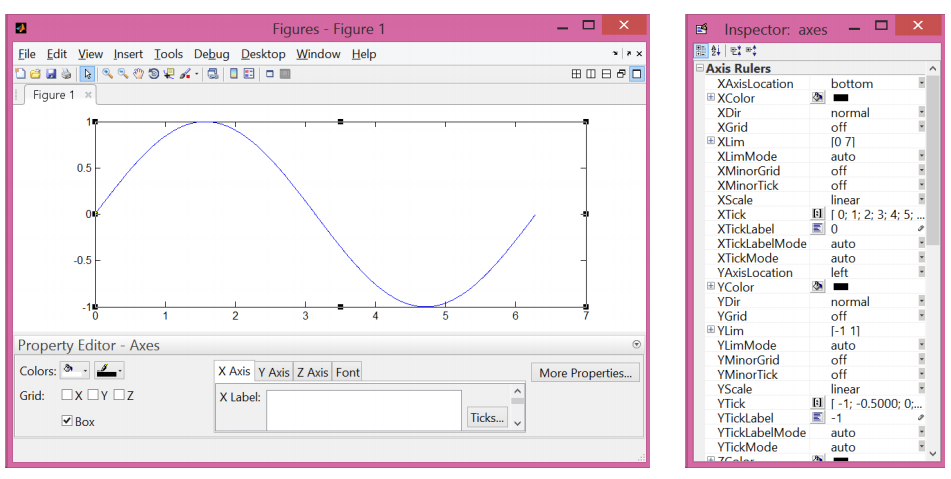
下面两个例子演示使用图形句柄操作图形对象:

1. 改变坐标轴属性:

   % 第一张图
   set(gca, 'FontSize', 25);
   
   % 第二张图
   set(gca, 'XTick', 0:pi/2:2*pi);
   set(gca, 'XTickLabel', 0:90:360);
   
   % 第三张图
   set(gca, 'FontName', 'symbol');
   set(gca, 'XTickLabel', {'0', 'p/2', 'p', '3p/2', '2p'});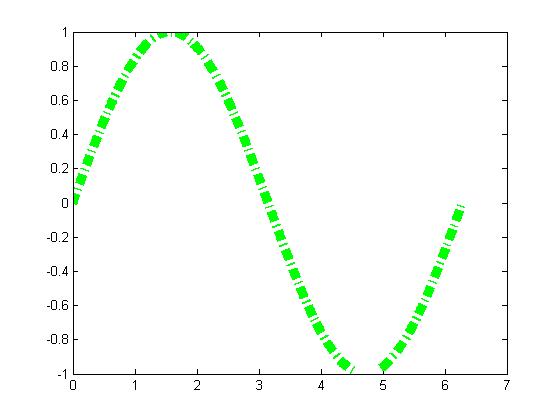

   

2. 改变线型

   h = plot(x,y); 
   set(h, 'LineStyle','-.', ...
   	'LineWidth', 7.0, ...
   	'Color', 'g');

   

将图形保存到文件

使用saveas(fig,filename)命令可以将图形对象保存到文件中,其中fig为图形句柄,filname为文件名.

saveas(gcf, 'myfigure.png')

绘制高级图表

二维图表

折线图

函数	图形描述
loglog()	x轴和y轴都取对数坐标
semilogx()	x轴取对数坐标,y轴取线性坐标
semilogy()	x轴取线性坐标,y轴取对数坐标
plotyy()	带有两套y坐标轴的线性坐标系
ploar()	极坐标系

对数坐标系图线

下面例子演示对数坐标系图线:

x = logspace(-1,1,100); y = x.^2;

subplot(2,2,1);
plot(x,y);
title('Plot');

subplot(2,2,2);
semilogx(x,y);
title('Semilogx');

subplot(2,2,3);
semilogy(x,y);
title('Semilogy');

subplot(2,2,4);
loglog(x, y);
title('Loglog');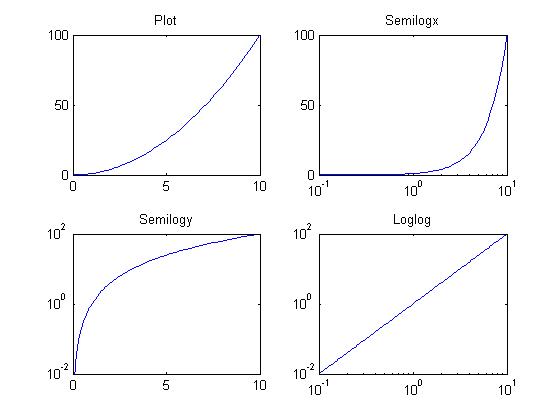 

对数坐标系可以加上网格,以区分线性坐标系与对数坐标系.

set(gca, 'XGrid','on');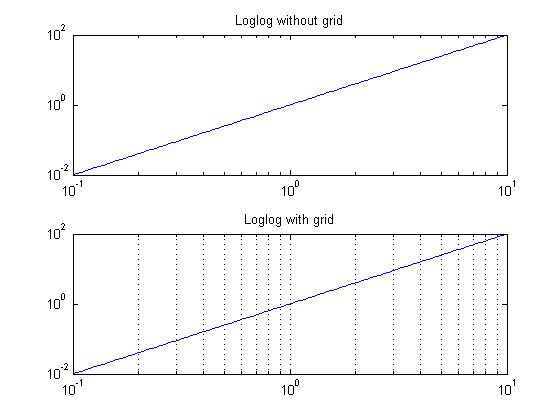

双y轴图线

plotyy()的返回值为数组[ax,hlines1,hlines2],其中:

• ax为一个向量,保存两个坐标系对象的句柄.
• hlines1和hlines2分别为两个图线的句柄.

x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
[AX,H1,H2] = plotyy(x,y1,x,y2);
set(get(AX(1),'Ylabel'),'String','Left Y-axis')
set(get(AX(2),'Ylabel'),'String','Right Y-axis')
title('Labeling plotyy');
set(H1,'LineStyle','--'); set(H2,'LineStyle',':');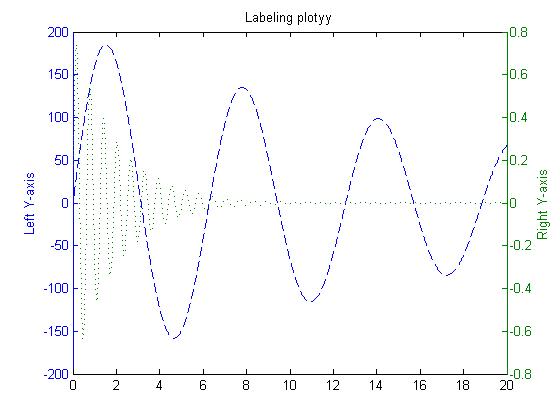

统计图表

函数	图形描述
hist()	直方图
bar()	二维柱状图
pie()	饼图
stairs()	阶梯图
stem()	针状图

直方图

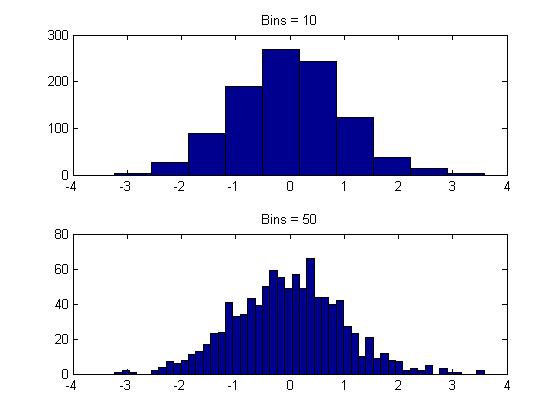
柱状图

• 使用bar()和bar3()函数分别绘制二维和三维直方图

  x = [1 2 5 4 8]; y = [x;1:5];
  subplot(1,3,1); bar(x); title('A bargraph of vector x');
  subplot(1,3,2); bar(y); title('A bargraph of vector y');
  subplot(1,3,3); bar3(y); title('A 3D bargraph');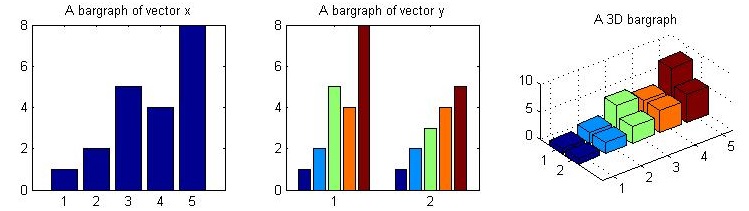

  

  hist主要用于查看变量的频率分布,而bar主要用于查看分立的量的统计结果.

• 使用barh()函数可以绘制纵向排列的柱状图

  x = [1 2 5 4 8];
  y = [x;1:5];
  barh(y);
  title('Horizontal');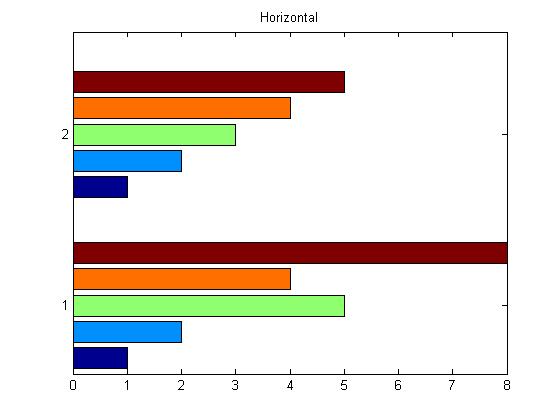

  

• 向bar()传入'stack'参数可以让柱状图以堆栈的形式画出.

  x = [1 2 5 4 8];
  y = [x;1:5];
  bar(y,'stacked');
  title('Stacked');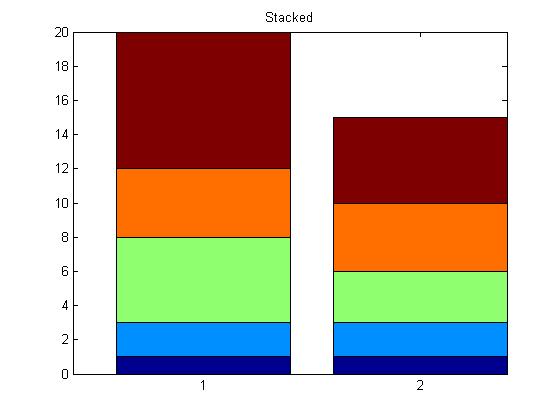

  

饼图

使用pie()和pie3()可以绘制二维和三维的饼图.向其传入一个bool向量表示每一部分扇区是否偏移.

a = [10 5 20 30];
subplot(1,3,1); pie(a);
subplot(1,3,2); pie(a, [0,0,0,1]);
subplot(1,3,3); pie3(a, [0,0,0,1]);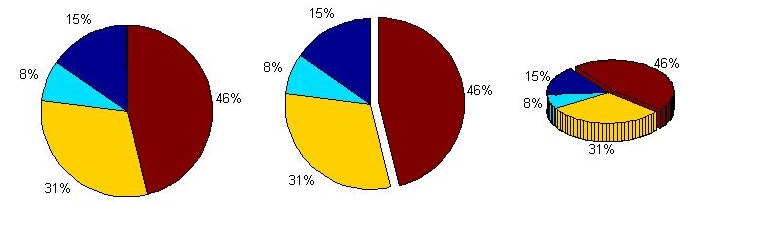

阶梯图和针状图:绘制离散数字序列

stairs()和stem()函数分别用来绘制阶梯图和针状图,用于表示离散数字序列.

x = linspace(0, 4*pi, 40); y = sin(x);
subplot(1,2,1); stairs(y);
subplot(1,2,2); stem(y);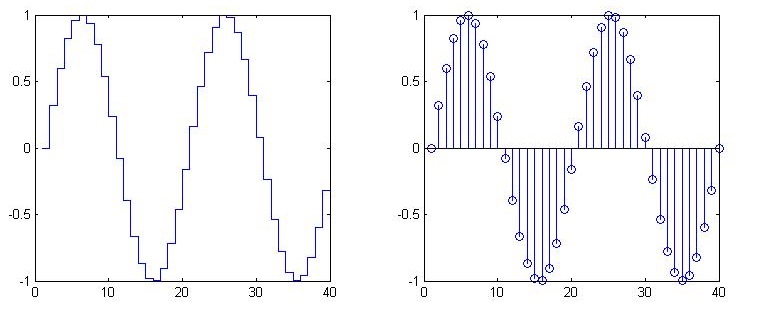

三维图表

二维图转为三维图

在MATLAB中,所有的图都是三维图,二维图只不过是三维图的一个投影.点击图形窗口的Rotate 3D按钮,即可通过鼠标拖拽查看该图形的三维视图.

三维图转换为二维图

使用imagesc()函数可以将三维图转换为二维俯视图,通过点的颜色指示高度.

[x, y] = meshgrid(-3:.2:3,-3:.2:3); z = x.^2 + x.*y + y.^2; 

subplot(1, 2, 1)
surf(x, y, z); 

subplot(1, 2, 2)
imagesc(z);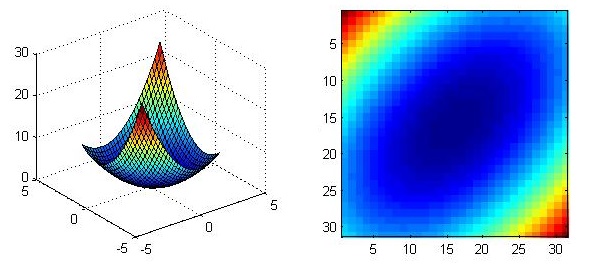

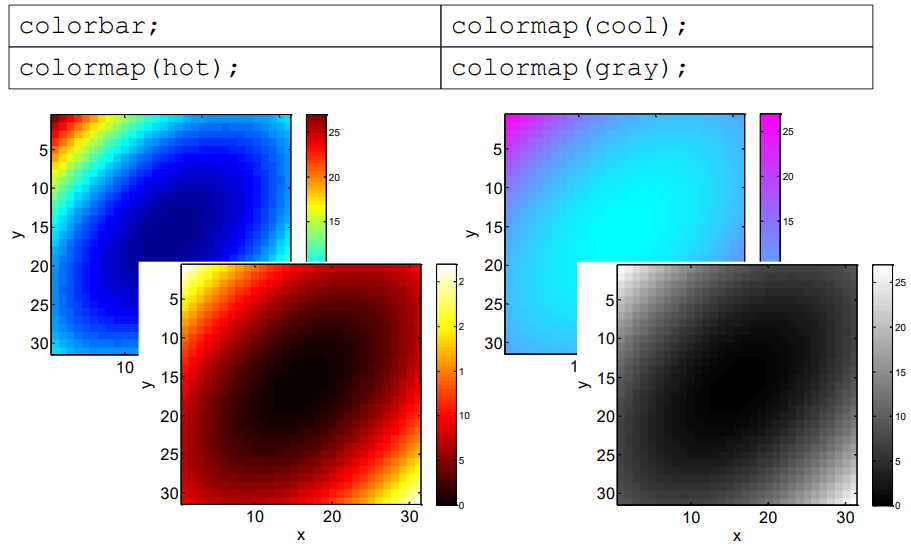
使用colorbar命令可以在生成的二维图上增加颜色与高度间对应关系的图例,使用colormap命令可以改变配色方案.具体细节请参考官方文档

三维图的绘制

绘制三维图前的准备工作

• 使用meshgrid()生成二维网格

meshgrid()函数将输入的两个向量进行相应的行扩充和列扩充以得到两个增广矩阵,对该矩阵可应用二元函数.

x = -2:1:2;
y = -2:1:2;
[X,Y] = meshgrid(x,y)
Z = X.^2 + Y.^2

绘制三维线

使用plot3()函数即可绘制三维面,输入应为三个向量.

x=0:0.1:3*pi; z1=sin(x); z2=sin(2.*x); z3=sin(3.*x);
y1=zeros(size(x)); y3=ones(size(x)); y2=y3./2;
plot3(x,y1,z1,'r',x,y2,z2,'b',x,y3,z3,'g'); grid on;
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');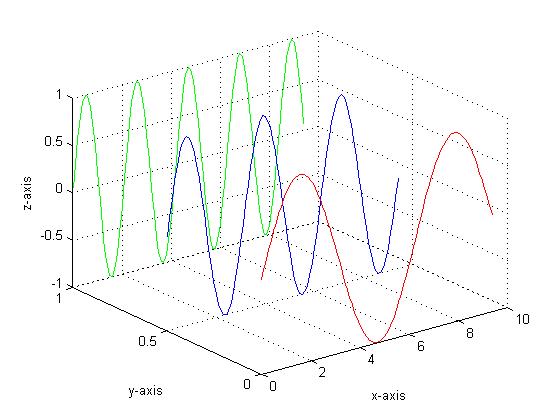

绘制三维面

使用mesh()和surf()命令可以绘制三维面,前者不会填充网格而后者会.

x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y);
Z = X.*exp(-X.^2-Y.^2);
subplot(1,2,1); mesh(X,Y,Z);
subplot(1,2,2); surf(X,Y,Z);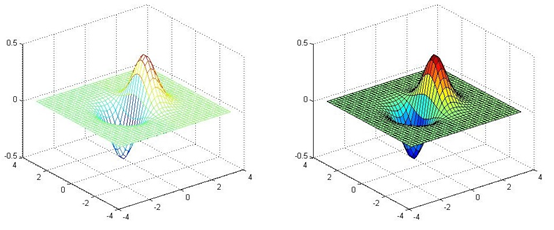

绘制三维图形的等高线

使用contour()和contourf()函数可以绘制三维图形的等高线,前者不会填充网格而后者会.

向contour()函数传入参数或操作图形句柄可以改变图像的细节:

x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2);

subplot(1,3,1); contour(Z,[-.45:.05:.45]); axis square;
subplot(1,3,2); [C,h] = contour(Z); clabel(C,h); axis square;
subplot(1,3,3); contourf(Z); axis square;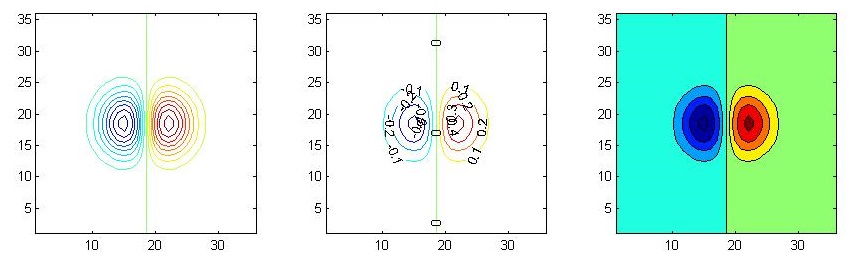

使用meshc()和surfc()函数可以在绘制三维图形时绘制其等高线.

x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;
[X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2);

subplot(1,2,1); meshc(X,Y,Z);
subplot(1,2,2); surfc(X,Y,Z);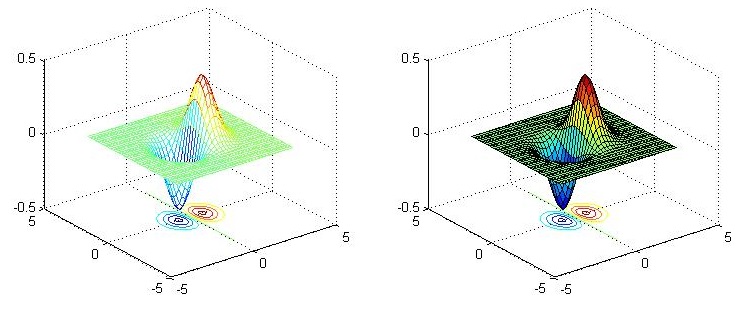

绘制三维体

使用patch()函数可以绘制三维体.

v = [0 0 0; 1 0 0 ; 1 1 0; 0 1 0; 0.25 0.25 1; 0.75 0.25 1; 0.75 0.75 1; 0.25 0.75 1];
f = [1 2 3 4; 5 6 7 8; 1 2 6 5; 2 3 7 6; 3 4 8 7; 4 1 5 8];

subplot(1,2,1); 
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(6), 'FaceColor', 'flat');
view(3); axis square tight; grid on;

subplot(1,2,2); 
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(8), 'FaceColor','interp');
view(3); axis square tight; grid on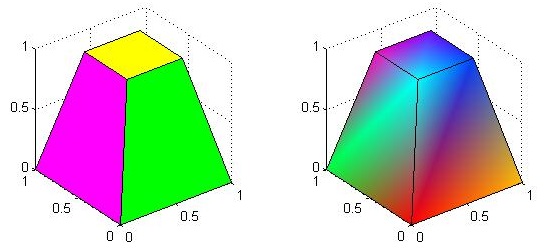

三维图的视角与打光

调整视角

使用view()函数可以调整视角,view()函数接受两个浮点型参数,分别表示两个方位角azimuth和elevation.

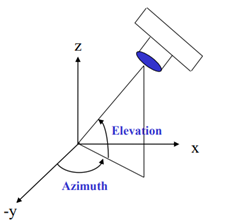
sphere(50); shading flat;
material shiny;
axis vis3d off;
view(-45,20);

符号运算

创建符号变量

创建符号数字

使用sym函数可以创建符号数字.使用符号数字可以精确地保存无理数,不会产生误差.

sym(1/3)	% 得到 1/3
1/3			% 得到 0.3333

将无理数保存为符号数字可以避免将其转换为浮点数的误差:

sin(sym(pi))	% 得到 0
sin(pi)			% 得到 1.2246e-16

创建符号变量

使用sym和syms可以创建符号变量,区别在于:

1. sym每次只能创建一个符号变量,而syms一次可以创建多个符号变量.

   syms a		% sym命令只能创建一个符号变量
   syms b c d	% syms命令可以创建多个符号变量

2. 若所指定的符号变量已存在,sym不会保留其原有的值,而syms会清空其值.

   syms x y
   f = x+y;	% 隐式创建符号变量f
   sym f		% 不清空变量f原有的值,即f = x + y

   syms x y
   f = x+y;	% 隐式创建符号变量f
   syms f		% 清空变量f原有的值,即f = f

3. 使用sym可以创建符号变量矩阵.

   A = sym('a', [2 5])	% 创建一个2*5的符号变量矩阵
   whos

   得到的输出如下:

   A =
   [ a1_1, a1_2, a1_3, a1_4, a1_5]
   [ a2_1, a2_2, a2_3, a2_4, a2_5]
    
    
     Name      Size            Bytes  Class    Attributes
     A         2x5               112  sym      

   联合使用sym和syms可以快速创建一系列带下标的变量

   clear all
   syms(sym('a', [1 5]))
   whos

   得到输出如下:

   Name      Size            Bytes  Class    Attributes
   a1        1x1                 8  sym                
   a2        1x1                 8  sym                
   a3        1x1                 8  sym                
   a4        1x1                 8  sym                
   a5        1x1                 8  sym                

符号运算

符号表达式的化简与代入

符号表达式的化简

使用simplify()函数可以化简符号表达式.

syms x a b c

simplify(sin(x)^2 + cos(x)^2);		% 得到 1
simplify(exp(c*log(sqrt(a+b))));	% 得到 (a + b)^(c/2)

表达式化简的标准是不确定的,下面三个函数分别按照不同标准化简表达式:

• expand()函数可以展开表达式

  syms x
  
  f = (x ^2- 1)*(x^4 + x^3 + x^2 + x + 1)*(x^4 - x^3 + x^2 - x + 1);
  expand(f);		% 得到 x^10 - 1

• factor()函数可以分解因式

  syms x
  
  g = x^3 + 6*x^2 + 11*x + 6;
  factor(g);		% 得到 (x + 3)*(x + 2)*(x + 1)

• horner()函数可以将多项式变为嵌套形式

  syms x
  
  h = x^5 + x^4 + x^3 + x^2 + x;
  horner(h);		% 得到 x*(x*(x*(x*(x + 1) + 1) + 1) + 1)

符号表达式的代入

使用sub(expr, old, new)函数可以将符号表达式expr中的old替换为new.

syms x y

f = x^2*y + 5*x*sqrt(y);
subs(f, x, 3);	% 得到 9*y + 15*y^(1/2)

求方程的解析解

使用solve(eqn,var)和solve(eqns,vars)可以求取方程式的解析解.

解单变量方程

使用==定义一个方程,并对其调用solve函数求解.（若不指定==符号右边的值,则默认等式右边为0.）

syms x

eqn = x^3 - 6*x^2 == 6 - 11*x;
solve(eqn);		% 得到 [1 2 3]

解多变量方程

对于多变量方程,我们需要指定针对哪个变量进行求解.

syms x y

eqn = [6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0];
solve(eqn, y);	% 得到 [1, 2*x, -3*x]

解方程组

向solve()函数传入方程组可以解方程.

syms u v

eqns = [2*u + v == 0, u - v == 1];
S = solve(eqns,[u v]);	

可以通过变量名索引方程的解,并可以将该解代入其他表达式中.

S.u;				% 得到 1/3
S.v;				% 得到 -2/3
subs(3*v + u, S);	% 得到 -3/5

符号微积分运算

求极限

使用limit(expr, var, a)函数可以求取符号表达式expr在变量var趋近于a时的极限,添加参数'left'或'right'可以指定左极限或右极限.

syms x;
expr = 1/x;

limit(expr,x,0);			% 得到NaN
limit(expr,x,0,'left');		% 得到-Inf
limit(expr,x,0,'right');	% 得到Inf

微分

使用diff(expr, var, n)函数可以求取符号表达式expr对变量var的n阶微分.

syms a b c x;
expr = a*x^2 + b*x + c;

diff(expr, a);		% 得到 x^2
diff(expr, b);		% 得到 x
diff(expr, x);		% 得到 b + 2*a*x
diff(expr, x, 2);	% 得到 2*a

积分

使用int(expr, var)函数可以求取符号表达式expr对变量var的不定积分.使用int(expr, var, [a, b])函数可以指定上下限求定积分,a和b可以是符号表达式.

syms x a b
expr = -2*x/(1+x^2)^2;

int(expr, x);			% 得到 1/(x^2 + 1)
int(expr, x, [1, 2]);	% 得到 -0.3
int(expr, x, [1, Inf]);	% 得到 -0.5
int(expr, x, [a, b]);	% 得到 1/(b^2 + 1) - 1/(a^2 + 1)

对于一些函数,MATLAB不能求出其积分,这时MATLAB会返回一个未解析(unsolved)的积分形式.

syms x
int(sin(sinh(x)));	% 一个无解的积分,MATLAB返回 int(sin(sinh(x)),

级数求和

使用symsum(expr, k, [a b])计算级数expr的索引k从a到b的加和.

syms k x

symsum(k^2, k)			% 得到 k^3/3 - k^2/2 + k/6
symsum(k^2, k, [0 10])	% 得到 385
symsum(x^k/factorial(k),k,1,Inf)	% 得到 exp(x) - 1

泰勒展开

使用taylor(expr,var,a)计算表达式expr在var=a处的泰勒级数.

syms x

taylor(exp(x))	% 得到 x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1
taylor(sin(x))	% 得到 x^5/120 - x^3/6 + x
taylor(cos(x))	% 得到 x^4/24 - x^2/2 + 1

绘制图像

可以对符号表达式绘制图像,常用的绘图函数如下:

函数	作用
fplot()	绘制符号表达式的二维线图像
fplot3()	绘制符号表达式的三维线图像
ezpolar()	绘制符号表达式的极坐标线图像
fmesh()	绘制网状面图像
fsurf()	绘制带颜色的面图像
fcontour()	绘制轮廓图像
fimplicit()	绘制隐含函数关系的图像

1. 下面例子展示二维和三维线图像的绘制

   subplot(1, 2, 1)
   syms x
   f = x^3 - 6*x^2 + 11*x - 6;
   fplot(f, x)
   
   subplot(1, 2, 2)
   syms t
   fplot3(t^2*sin(10*t), t^2*cos(10*t), t)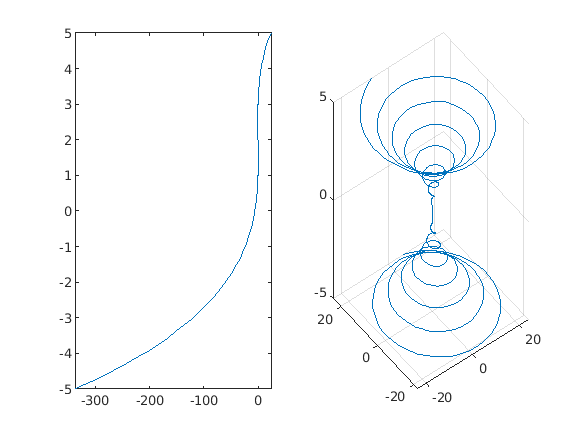

   

2. 下面例子演示三维面的绘制

   syms x y
   fsurf(x^2 + y^2)

   

3. 下面例子演示隐含函数关系图像的绘制

   syms x y
   eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2;
   fimplicit(eqn, [-1 1])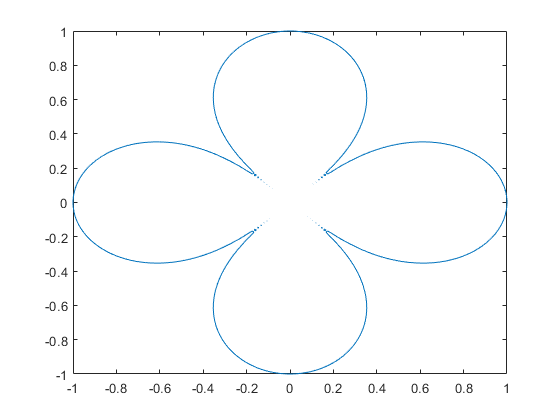

   

数值计算

多项式的数值运算

使用MATLAB表示多项式

使用向量表示多项式

在MATLAB中,多项式可以用向量表示,向量中的元素为多项式的系数(降幂排序):第一位为多项式最高次项系数,最后一位为常数项.

例如多项式:
f(x) = x^3 - 2x - 5f(x)=x3−2x−5

可以用向量p = [1 0 -2 -5]表示.

多项式求值:polyval()

使用polyval(p, x)可以计算多项式p在x的每个点处的值.

a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f);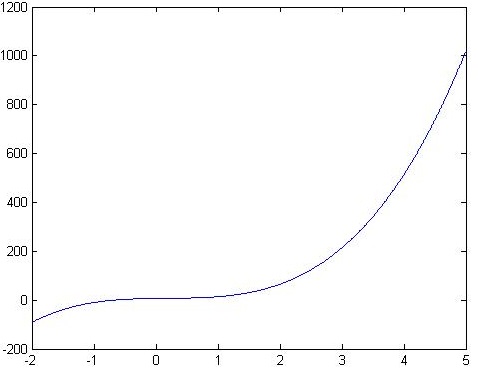

多项式的乘法:conv()

使用conv(p1, p2)函数可以对两个向量p1和p2进行卷积相乘,用于计算多项式的乘法.

例如多项式:
f(x) = (x^2+1) (2x+7)f(x)=(x2+1)(2x+7)

可以使用conv()函数得到展开后的多项式:

p = conv([1 0 1], [2 7])

得到p = [2 7 2 7].

多项式的数值运算

多项式的因式分解:roots()

使用roots(p)函数可以对多项式p进行因式分解,即求表达式值为0的根.

p = roots([1 -3.5 2.75 2.125 -3.875 1.25])

得到p = [2 -1, 1+0.5i, 1-0.5i, 0.5],表示x^5 -3.5 x^4 +2.75 x^3 + 2.125 x^2 + -3.875 x+1.25 = (x-2)(x+1)(x-1-0.5i)(x-1+0.5i)(x-0.5)x5−3.5x4+2.75x3+2.125x2+−3.875x+1.25=(x−2)(x+1)(x−1−0.5i)(x−1+0.5i)(x−0.5).

多项式的微分:polyder()

使用polyder(p)函数可以计算多项式的导数.

例如对下面多项式求导:
f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1

p = polyder([5 0 -2 0 1]);

得到p = [20 0 -4 0],表示计算得到导数f’(x) = 20 x^3 - 4xf′(x)=20x3−4x.

多项式的积分:polyint()

使用polyint(p, k)函数可以计算多项式p的积分,积分结果的常数项设为k.

例如对下面多项式求导:
f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1

p = polyint([5 0 -2 0 1], 3)

得到p = [1 0 -0.6667 0 1 3],表示计算得到积分\int f(x) dx = x^5 -0.6667x^3 + x + 3∫f(x)dx=x5−0.6667x3+x+3.

非线性表达式的数值运算

方程(组)求根fsolve()

使用fsolve(fun, x0)求非线性方程组的根,fun为待求方程的函数句柄,x0为初值.

1. 求方程1.2x+x\sin(x)+0.3=01.2x+xsin(x)+0.3=0在x=0x=0附近的解.

   f2 = @(x) (1.2*x+x*sin(x)+0.3);
   fsolve(f2,0)	% 得到 -0.3500

2. 解方程组
   \begin{aligned} \left{ \begin{aligned} e^{-e^{-(x_1+x_2)}} - x_2(1+x_1^2) = 0 \ x_1 \cos x_2 + x_2 \sin x_1 - \frac{1}{2} = 0 \end{aligned} \right. \end{aligned}⎩⎪⎨⎪⎧​e−e−(x1​+x2​)−x2​(1+x12​)=0x1​cosx2​+x2​sinx1​−21​=0​​

   设定初值为[0, 0][0,0]

   fun = @(x) [exp(-exp(-(x(1)+x(2))))-x(2)*(1+x(1)^2)...
       x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5]
   x0 = [0,0];
   x = fsolve(fun,x0)	% 得到[0.3532 0.6061]

数值微分

求差分:diff()

使用diff(X, n)计算向量X的n阶差分,n默认为1.

x = [1 2 5 2 1];
diff(x);	% 得到 [1 3 -3 -1]
diff(x,1);	% 得到 [1 3 -3 -1]
diff(x,2);	% 得到 [2 -6 2]

求导数:diff(y)./diff(x)

使用导数的定义

$$f'(x_0) = \lim_{h\rarr 0} \frac{f(x_0 + h) - f(x_0)}{h}$$$

可以计算函数在某点的近似导数.

下面程序计算f(x) = x^3f(x)=x3的一阶和二阶导数的值.

x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x);			% 计算一阶导数
m2 = diff(m)./diff(x(1:end-1));	% 计算二阶导数

plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x'); ylabel('y');
legend('f(x) =x^3','f''(x)','f''''(x)', 4);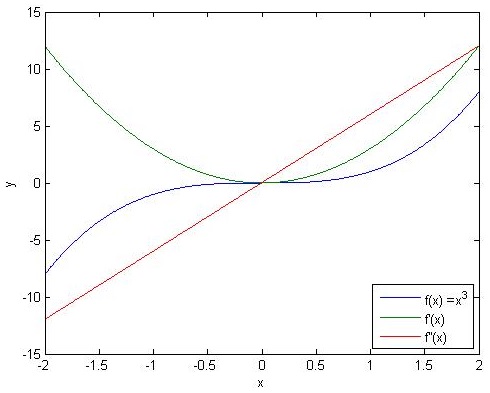

数值积分

数值积分原理

有三种常见算法用于计算数值积分: 矩形法,梯形法,抛物线法,它们分别把微分区间的图形视为矩形,梯形,抛物线以计算面积.

算法	图示	表达式
矩形法(Midpoint Rule)		$\int_a^b f(x) dx = 2h \sum_{i=0}^{(n/2)-1} f(x_{2i+1})$
梯形法(Trapezoid Rule)		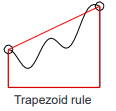$\int_a^b f(x) dx = \frac{h}{2} \left[ f(a) + 2\sum_{i=1}^{n-1} f(x_i) +f(b) \right]$
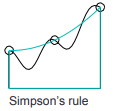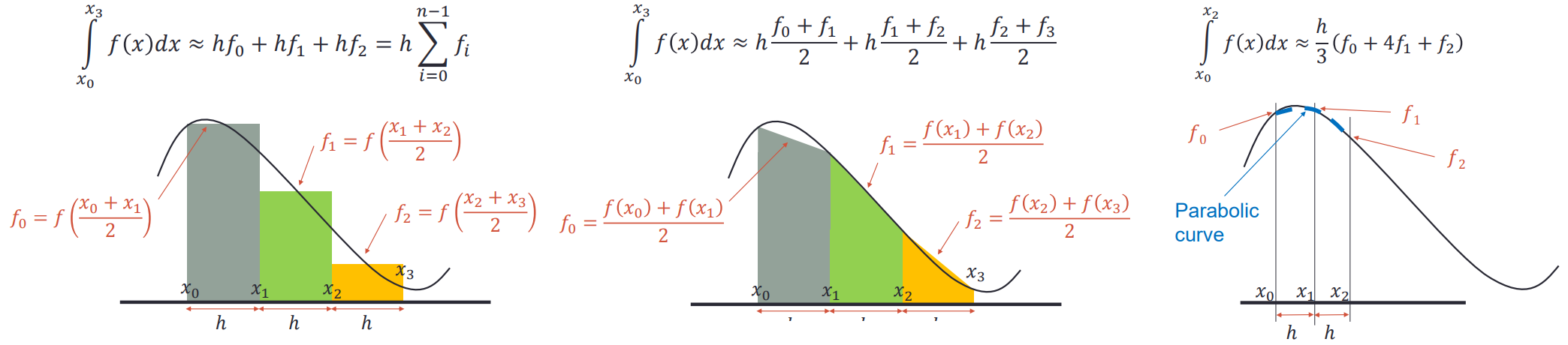
抛物线法(Simpson’s Rule)		$\int_a^b f(x) dx = \frac{h}{3} \left[ f(a) + 2\sum_{i=1}^{(n/2)-1} f(x_{2i}) + 4\sum_{i=1}^{n/2} f(x_{2i-1}) + f(b) \right]$

下面分别使用三种方法计算f(x) = 4x^3f(x)=4x3在区间(0, 2)(0,2)内的积分.

h = 0.05; x = 0:h:2;


% 使用矩形法计算近似积分
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y)			% 得到 15.9950

% 使用梯形法计算近似积分
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid)	% 得到 15.2246

% 使用抛物线法计算数值积分
s = h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end))	% 得到 15.8240

数值积分函数:integral()

integral(),integral2(),integral3()分别对函数在xmin至xmax间进行一重,二重,三重积分.

它们的第一个参数都应该是一个函数句柄,下面例子演示他们的用法:

1. 计算\int_0^2 \frac{1}{x^3-2x-5}∫02x3−2x−51

   f = @(x) 1./(x.^3-2*x-5);
   integral(f,0,2)		% 得到 -0.4605

2. 计算\int0^\pi \int\pi^{2\pi} (y\sin(x) + x \cos(y)) dx dy∫0π∫π2π(ysin(x)+xcos(y))dxdy

   f = @(x,y) y.*sin(x)+x.*cos(y);
   integral2(f,pi,2*pi,0,pi)	% 得到 -9.8696

3. 计算\int_{-1}^1 \int_0^1 \int_0^\pi (y\sin(x) + z \cos(y)) dx dy dz∫−11∫01∫0π(ysin(x)+zcos(y))dxdydz

   f = @(x,y,z) y.*sin(x)+z.*cos(y);
   integral3(f,0,pi,0,1,-1,1)

统计与拟合

统计

描述性统计(Descriptive Statistics)

描述性统计主要研究数据的中心趋势(Central Tendency)和Variation

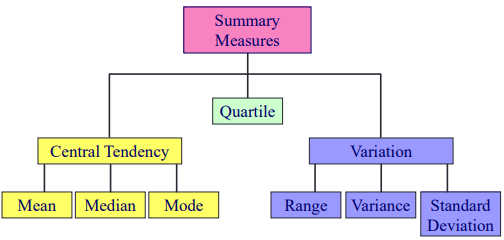
中心趋势(Central Tendency)

函数	作用
mean()	计算平均值
median()	计算中位数
mode()	计算众数
prctile(X,num)	数据X的num%分位数为多少
max()	计算最大值
min()	计算最小值

下列函数绘制统计图表:

函数	作用
bar()	绘制条形图
stem()	绘制针状图
area()	绘制填充图
boxplot()	绘制箱线图

x = 1:14;
freqy = [1 0 1 0 4 0 1 0 3 1 0 0 1 1];
subplot(1,3,1); bar(x,freqy); xlim([0 15]);
subplot(1,3,2); area(x,freqy); xlim([0 15]);
subplot(1,3,3); stem(x,freqy); xlim([0 15]);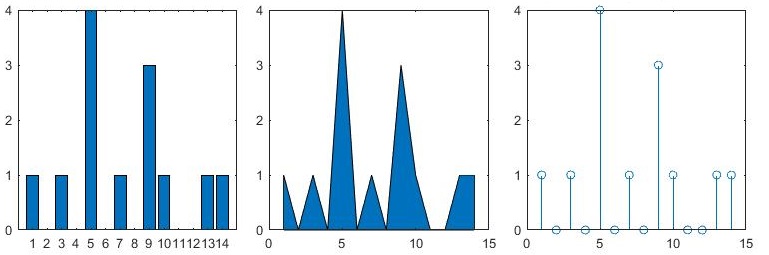

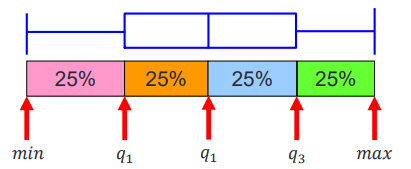
箱线图可以突出显示数据的四分位点.

marks = [80 81 81 84 88 92 92 94 96 97];
boxplot(marks) 
% prctile(marks, [25 50 75])	% 得到 [81 90 94]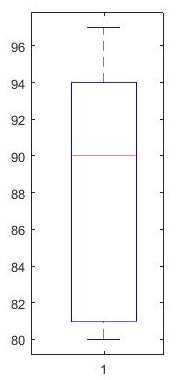

Variation

离散程度

函数	作用
std()	计算数据的标准差
var()	计算数据的方差

偏度(Skewness

函数	作用
skewness()	计算数据的偏度

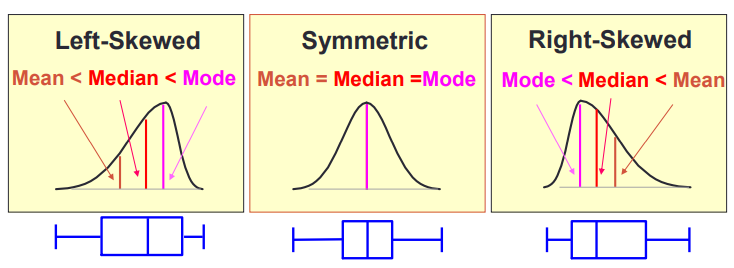
偏度反映数据的对称程度

• 数据左偏时,其偏度小于0.
• 数据完全对称时,其偏度等于0.
• 数据右偏时,其偏度大于0.

X = randn([10 3]);		% 构造10*3的矩阵
X(X(:,1)<0, 1) = 0; 	% 将第一列数据右偏
X(X(:,3)>0, 3) = 0;		% 将第二列数据左偏
boxplot(X, {'Right-skewed', 'Symmetric', 'Left-skewed'});
skewness(X);	% 得到 [0.5162 -0.7539 -1.1234]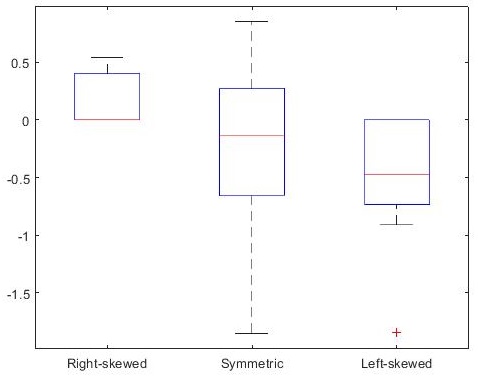

峰度(Kurtosis)

函数	作用
kurtosis()	计算数据的峰度

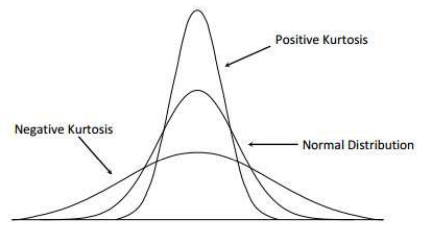
峰度(Kurtosis)表征概率密度分布曲线在平均值处峰值的高低.直观来看,峰度反映了峰部的尖度.

统计推断(Inferential Statistics)

推论统计的核心即为假设检验.下列函数用于进行假设检验.

函数	作用
ttest()	进行T检验
ztest()	进行Z检验
ranksum()	进行秩和检验
signrank()	进行符号秩检验

load examgrades
x = grades(:,1);
y = grades(:,2);
[h,p] = ttest(x,y);

执行上述程序,得到[h p] = [0 0.9805],表示在默认显著性水平(5%)下我们没有理由拒绝x与y同分布.

拟合

多项式拟合

一元多项式拟合:polyfit()

使用polyfit(x, y, n)函数对数据x和y进行n次多项式拟合.

x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];

for i = 1:3 % 分别进行一次,二次,三次拟合
    p = polyfit(x, y, i);
    xfit = x(1):0.1:x(end); yfit = polyval(p, xfit);
    subplot(1, 3, i); plot(x, y, 'ro', xfit, yfit);
    legend('Data points', 'Fitted curve', 'Location', 'southeast');
end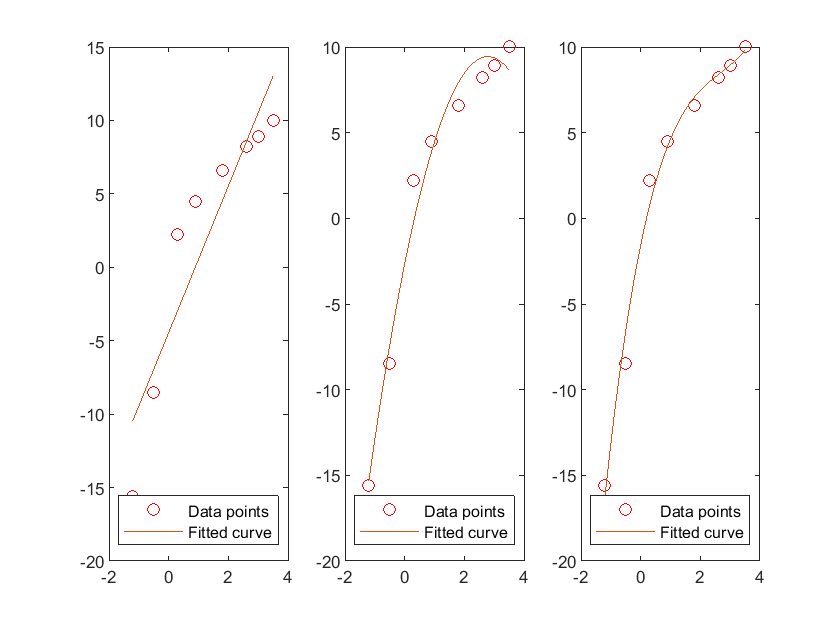

多元线性拟合:regress()

使用regress(y, X)函数对数据X和y进行多元线性回归.

load carsmall;
y = MPG; x1 = Weight; x2 = Horsepower;		% 导入数据集
X = [ones(length(x1),1) x1 x2];				% 构建增广X矩阵
b = regress(y,X);							% 进行线性回归

% 下面是绘图语句
x1fit = min(x1):100:max(x1); x2fit = min(x2):10:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = b(1)+b(2)*X1FIT+b(3)*X2FIT;
scatter3(x1,x2,y,'filled'); hold on;
mesh(X1FIT,X2FIT,YFIT); hold off;
xlabel('Weight'); ylabel('Horsepower'); zlabel('MPG'); view(50,10);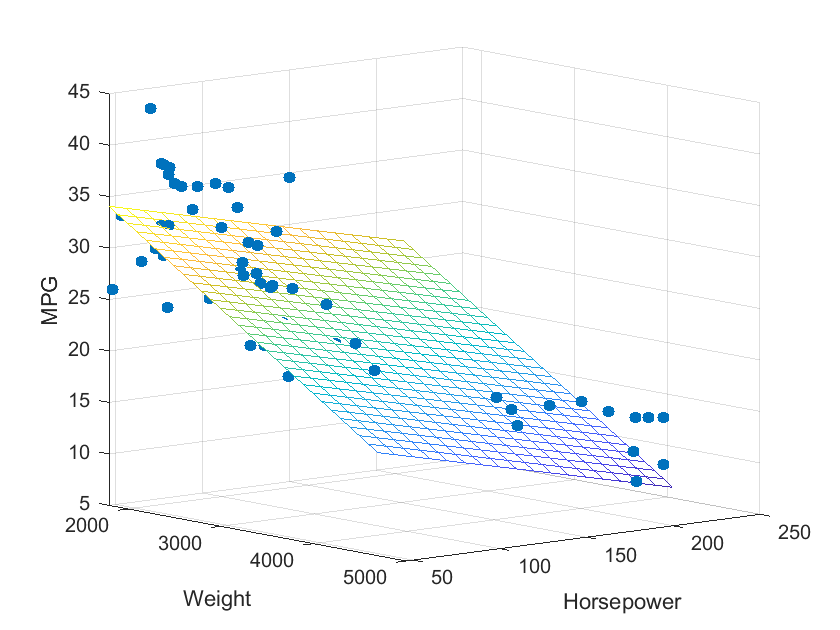

非线性拟合

对于非线性拟合,需要使用曲线拟合工具箱.在命令窗口输入cftool()打开曲线拟合工具箱.

插值

一维插值

函数	作用
interp1(x,v)或interp1(x,v,xq)	线性插值
spline(x,v)或spline(x,v,xq)	三次样条插值
pchip(x,v)或pchip(x,v,xq)	三次Hermite插值
mkpp(breaks,coefs)	生成分段多项式
ppval(pp,xq)	计算分段多项式的插值结果

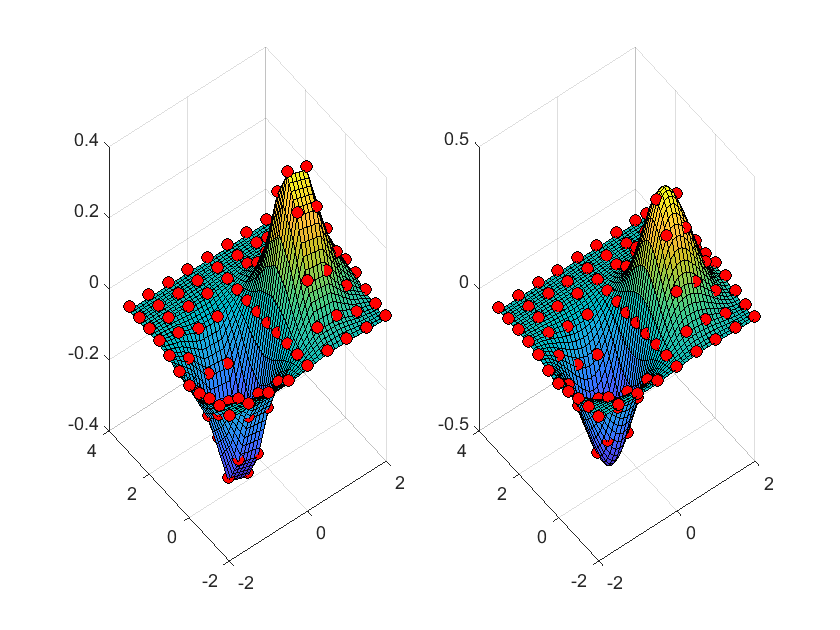
下面例子演示使用interp1(x, v, xq)进行线性插值和使用spline(x, v, xq)进行三次样条插值.各参数意义如下:

• x,v: 待插值样本点.
• xq: 查询点,函数返回在这些点处的插值结果.

% 构造数据
x = linspace(0, 2*pi, 40); x_m = x; x_m([11:13, 28:30]) = NaN; 
y_m = sin(x_m);
plot(x_m, y_m, 'ro', 'MarkerFaceColor', 'r'); hold on; 	

% 对数据进行线性插值
m_i = ~isnan(x_m);
y_i = interp1(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-b'); hold on;

% 对数据进行三次样条插值
m_i = ~isnan(x_m);
y_i = spline(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-g'); 

legend('Original', 'Linear', 'Spline');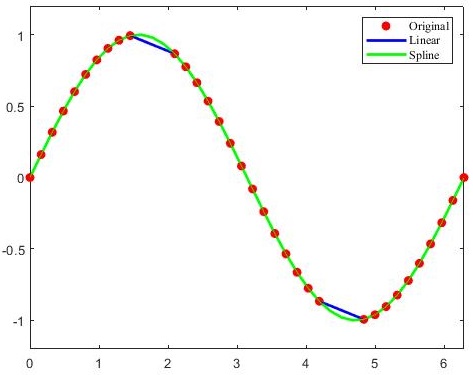

二维插值

使用interp2()可以进行二维插值,向其method参数传入字符串可以指定插值算法.

方法	说明	连续性
'linear'	(默认)在查询点插入的值基于各维中邻点网格点处数值的线性插值.	C0
'spline'	在查询点插入的值基于各维中邻点网格点处数值的三次插值.插值基于使用非结终止条件的三次样条.	C2
'nearest'	在查询点插入的值是距样本网格点最近的值.	不连续
'cubic'	在查询点插入的值基于各维中邻点网格点处数值的三次插值.插值基于三次卷积.	C1
'makima'	修改后的Akima三次Hermite插值.在查询点插入的值基于次数最大为3的多项式的分段函数,使用各维中相邻网格点的值进行计算.为防过冲,已改进 Akima 公式.	C1

% 构建样本点
xx = -2:.5:2; yy = -2:.5:3; [x,y] = meshgrid(xx,yy); 
xx_i = -2:.1:2; yy_i = -2:.1:3; [x_i,y_i] = meshgrid(xx_i,yy_i);
z = x.*exp(-x.^2-y.^2);

% 线性插值
subplot(1, 2, 1); 
z_i = interp2(xx,yy,z,x_i,y_i);
surf(x_i,y_i,z_i); hold on;
plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on;

% 三次插值
subplot(1, 2, 2); 
z_ic = interp2(xx,yy,z,x_i,y_i, 'spline');
surf(x_i,y_i,z_ic); hold on;
plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on;