美赛校选培训课笔记

多元统计分析

聚类分析

特点：

• 事先不知道类别的个数与结构；
• 进行分析的数据是对象间的相似性或相异性（距离）；
• 将距离近的对象归入一类。

分类

• 根据分类对象不同分为

  • Q型聚类：对样本进行聚类

  • R型聚类：对变量进行聚类

• 根据聚类方法主要分为

  • 系统聚类法
  • 动态聚类法

距离

Minikowski距离：

$$d(x,y) = [\sum\limits_{k=1}^p|x_{k} - y_{k}|^{m}]^{\frac{1}{m}}， x,y为p维列向量$$

• m = 1时，为绝对距离
• m = 2时，为欧氏距离
• m = $\infty$, 为切比雪夫距离，即 $\mathop{max}\limits{1\le k \le p}|x{k} - y_{k}|$

Mahalanobis距离(聚类分析中常用)

$$d(x,y) = \sqrt{(x - y)^{T} \sum\nolimits^{-1} (x - y)}$$

其中x, y为来自 p 维总体Z的样本观测值，Σ为Z 的协方差矩阵，实际中Σ往往是不知道的，常常需要用样本协方差来估计。马氏距离对一切线性变换是不变的，故不受量纲的影响。

R语句：

dist(x,method=“euclidean”, diag=FALSE, upper=FALSE, p=2)

• method: 计算距离的方法

  • “euclidean”: 欧式距离

  • “maximum”: Chebyshev距离

  • “manhattan”: 绝对值距离

  • “minkowski”: Minkowski距离，p是Minkowski距离的阶数

• diag=TRUE: 输出对角线上的距离

• upper=TRUE: 输出上三角矩阵的值（默认值仅输出下 三角矩阵的值）

python语句：

import rpy2.robjects as robjects

x = [1, 2, 6, 8, 11]
r = robjects.r
res = r.dist(x)
print(res)
#    1  2  3  4
# 2  1
# 3  5  4
# 4  7  6  2
# 5 10  9  5  3

import rpy2
import rpy2.robjects.numpy2ri

R = rpy2.robjects.r
r_code = """
x<-c(1,2,6,8,11)
y<-dist(x)
print(y)
"""
R(r_code)

• 注：我用rpy2来实现这个感觉比较费劲。可能不太能从python 调用R语言，建议直接用R语言吧

标准化处理

当指标的测量值相差悬殊时，应先对数据进行标准化处理，再利用标准化的数据计算距离。

普通标准化变换

$$X_{ij}^{*} = \frac{X_{ij} - \overline{X}_{j}}{S_{j}}$$

i=1,2,…n表示第i个样本，j=1,2,…p表示样本的第j个指标，每个样本均有p个观测指标. 是第j个指标的样本均值

极差标准化变换

$$X_{ij}^{*} = \frac{X_{ij} - \overline{X}_{j}}{R_{j}} \\ 其中，R_{j} = \mathop{\max}\limits_{1\le k \le n}X_{kj} - \mathop{\max}\limits_{1 \le k \le n}X_{kj}$$

极差正规化变换

$$X_{ij}^{*} = \frac{X_{ij} - \mathop{\min}\limits_{1\le k\le n} X_{kj}}{R_{j}}$$

程序语句

数据的中心化和标准化处理

R语句

scale(X,center = True, scale = True)

X:样本数据矩阵，center = TURE表示对数据做中心化变换，scale=TRUE表示对数据做标准化变化

python语句

import rpy2
import numpy
import rpy2.robjects.numpy2ri

rpy2.robjects.numpy2ri.activate()

R = rpy2.robjects.r
x = numpy.array([[1.0, 2.0], [3.0, 1.0]])
res = R.scale(x, center=True, scale=True)
print(res)

数据做极差标准化处理

x <- data.frame(
    points = c(99, 97, 104, 79, 84, 88, 91, 99),
    rebounds = c(34, 40, 41, 38, 29, 30, 22, 25),
    blocks = c(12, 8, 8, 7, 8, 11, 6, 7)
)
# apply（）函数必须应用于dataframe或matrix
center <- sweep(x, 2, apply(x, 2, mean))
R <- apply(x, 2, max) - apply(x, 2, min)
x_star <- sweep(center, 2, R, "/")
# 若x_star<-sweep(center, 2, sd(x), "/"), 则得到（普通）标准化变换后的数据；
print(x_star)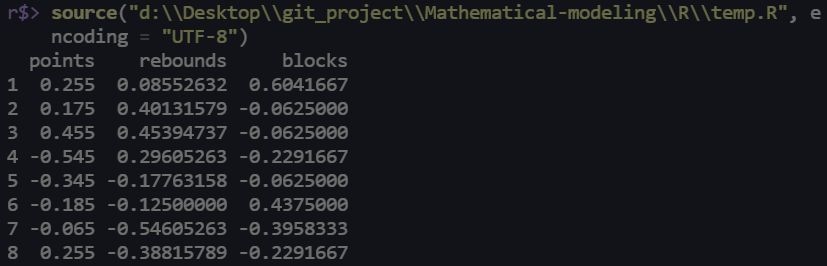

sweep(x, MARGIN, STATS, FUN=”-“, …)

• x:数组或矩阵；MARGIN:运算区域，对矩阵1表示行，2表示列；

• STATS是统计量，apply(x, 2, mean)表示各列的均值；

• FUN表示函数的运算，缺省值为减法运算。

相似系数

计算样本不同指标间的相关系数，适用于对变量进行聚类。

系统聚类法

聚类分析方法中最常用

基本思想

• （1）视各样本（或变量）自成一类，规定类与类之间的距离（或相似系数）；
• （2）把最相似的样本（或变量）聚为小类，再将已聚合的小类按相似性再聚合；
• （3）最后将一切子类都聚合到一个大类，从而得到一个按相似性大小聚集起来的谱系关系

3.根据距离定义的不同分为

• （1）最短距离法：类与类之间的距离定义为两类中最近样本间的距离；
• （2）最长距离法：类与类之间的距离定义为两类中最远样本间的距离；
• （3）类平均法：类与类之间的距离定义为两类中两两样本间距离的平均数；

程序

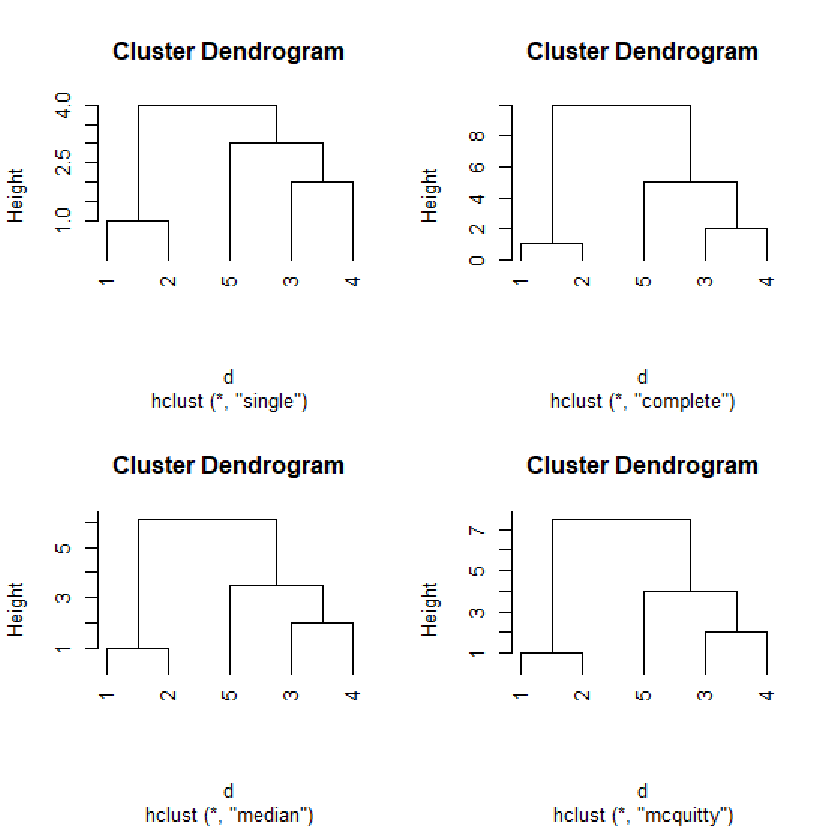
 x<-c(1,2,6,8,11); 
dim(x)<-c(5,1); 
d<-dist(x) #生成距离结构
hc1<-hclust(d, "single"); hc2<-hclust(d, "complete")
hc3<-hclust(d, "median"); hc4<-hclust(d, "mcquitty") #生成系统聚类
opar <- par(mfrow = c(2, 2))
plot(hc1,hang=-1); plot(hc2,hang=-1)
plot(hc3,hang=-1); plot(hc4,hang=-1)
par(opar)#  画出所有树形结构图，以2*2的形式画在一张图上

hclust():进行系统聚类的计算
plot():画出系统聚类的树形图
hclust(d, method = “complete”)
d:dist构成的距离结构，
method:系统聚类的方法（默认为最长距离法），其参数有：
（1）“single”：最短距离法
（2）“complete”：最长距离法
（3）“average”：类平均法
……
plot(x, labels = NULL, hang = 0.1, main = “Cluster
Dendrogram”, sb = NULL, xlab = NULL, ylab =”Height”, …)

x: hclust()函数生成的对象
hang: 表明树形图中各类的位置，取负值表示树形图中的类从底部画起
main: 绘图名称

动态聚类法

系统聚类：一次形成类后就不再改变；
动态聚类：逐步聚类

基本思路

首先粗略分类，然后按某种最优原则修改不合理的分类，直至分得比较合理为止，形成最终分类结果。

程序

kmeans(x, centers, iter.max=10, nstart=1, algorithm*=c(“Hartigan-Wong”, “Lloyd”, “MacQueen”))

• x是由数据构成的矩阵或数据框，
• centers是聚类的个数或者初始类的中心，
• iter.max为最大迭代次数（最大值为10），
• nstart是随机集合的个数，
• algorithm是动态聚类的算法。

X<-data.frame(
   x1=c(2959.19, 2459.77, 1495.63, 1046.33, 1303.97, 1730.84, 1561.86, 1410.11, 3712.31, 2207.58, 2629.16, 1844.78, 2709.46, 1563.78, 1675.75, 1427.65, 1783.43, 1942.23, 3055.17, 2033.87, 2057.86, 2303.29, 1974.28, 1673.82, 2194.25, 2646.61, 1472.95, 1525.57, 1654.69, 1375.46, 1608.82), 
   x2=c(730.79, 495.47, 515.90, 477.77, 524.29, 553.90, 492.42, 510.71, 550.74, 449.37, 557.32, 430.29, 428.11, 303.65, 613.32, 431.79, 511.88, 512.27, 353.23, 300.82, 186.44, 589.99, 507.76, 437.75, 537.01, 839.70, 390.89, 472.98, 437.77, 480.99, 536.05),
   x3=c(749.41, 697.33, 362.37, 290.15, 254.83, 246.91, 200.49, 211.88, 893.37, 572.40, 689.73, 271.28, 334.12, 233.81, 550.71, 288.55, 282.84, 401.39, 564.56, 338.65, 202.72, 516.21, 344.79, 461.61, 369.07, 204.44, 447.95, 328.90, 258.78, 273.84, 432.46), 
   x4=c(513.34, 302.87, 285.32, 208.57, 192.17, 279.81, 218.36, 277.11, 346.93, 211.92, 435.69, 126.33, 160.77, 107.90, 219.79, 208.14, 201.01, 206.06, 356.27, 157.78, 171.79, 236.55, 203.21, 153.32, 249.54, 209.11, 259.51, 219.86, 303.00, 317.32, 235.82),
   x5=c(467.87, 284.19, 272.95, 201.50, 249.81, 239.18, 220.69, 224.65, 527.00, 302.09, 514.66, 250.56, 405.14, 209.70,272.59, 217.00, 237.60, 321.29, 811.88, 329.06, 329.65, 403.92, 240.24, 254.66, 290.84, 379.30, 230.61, 206.65, 244.93, 251.08, 250.28),
   x6=c(1141.82, 735.97, 540.58, 414.72, 463.09, 445.20, 459.62, 376.82, 1034.98, 585.23, 795.87, 513.18, 461.67, 393.99, 599.43, 337.76, 617.74, 697.22, 873.06, 621.74, 477.17, 730.05, 575.10, 445.59, 561.91, 371.04, 490.90, 449.69, 479.53, 424.75, 541.30),
   x7=c(478.42, 570.84, 364.91, 281.84, 287.87, 330.24, 360.48, 317.61, 720.33, 429.77, 575.76, 314.00, 535.13, 509.39, 371.62, 421.31, 523.52, 492.60, 1082.82, 587.02, 312.93,438.41, 430.36, 346.11, 407.70, 269.59, 469.10, 249.66, 288.56, 228.73, 344.85),
   x8=c(457.64, 305.08, 188.63, 212.10, 192.96, 163.86, 147.76, 152.85, 462.03, 252.54, 323.36, 151.39, 232.29, 160.12, 211.84, 165.32, 182.52, 226.45, 420.81, 218.27, 279.19, 225.80, 223.46, 191.48, 330.95, 389.33, 191.34, 228.19, 236.51, 195.93, 214.40),
   row.names = c("北京", "天津", "河北", "山西", "内蒙古", "辽宁", "吉林", "黑龙江", "上海", "江苏", "浙江", "安徽", "福建", "江西", "山东",  "河南", "湖北", "湖南", "广东", "广西", "海南", "重庆", "四川", "贵州", "云南", "西藏", "陕西", "甘肃", "青海", "宁夏", "新疆")
)

kmeans(scale(X),5)


K-means clustering with 5 clusters of sizes 10, 7, 3, 7, 4


Clustering vector:
  北京   天津   河北   山西 内蒙古   辽宁   吉林 黑龙江   上海   江苏 
     5      4      3      3      3      3      3      3      5      4 
  浙江   安徽   福建   江西   山东   河南   湖北   湖南   广东   广西 
     5      1      2      1      4      1      1      4      5      2 
  海南   重庆   四川   贵州   云南   西藏   陕西   甘肃   青海   宁夏 
     2      4      1      1      4      4      1      3      3      3 
  新疆
     3

主成分分析法

基本思想

实际问题中的变量的重要性有所不同，且众多变量间有一定的相关关系。通过这种相关性对这些变量加以改造，用为数较少的新变量反映原变量提供的大部分信息，简化原问题。即数据降维

主成分分析法就是在这种降维思想下产生的处理高维数据的统计方法。

基本方法

通过适当构造原变量的线性组合，产生一列互不相关的新变量，从中选出少数几个新变量并使它们含有尽可能多的原变量带有的信息，从而使用少数几个新变量代替原变量，以分析原问题。

变量中所含“信息”的大小通常用该变量的方差或样本方差来度量。

如常数a,Var(a) = 0 ,我们通过a，只能知道a这个常数，其所含信息少。

主成分的定义

设$X = (X{1}, X{2},……,X_{p})^{T}$为实际问题涉及的p个随机变量构成的向量，记X的均值为$\mu$，协方差阵为$\sum$.

考虑线性组合

$$\left\{ \begin{aligned} Y_{1} & = & a_{1}^{T}X \\ . \\ . \\ Y_{p} & = & a_{p}^{T}X \\ \end{aligned} \right.$$

………………………………………………………………………………………………………

warning： 直接写代码了

程序

求矩阵的特征值和特征向量

a <- c(1, -2, 0, -2, 5, 0, 0, 0, 2)
# 由向量a构造一3列的矩阵， byrow=T表示生成矩阵的数据按行放置；
b <- matrix(data = a, ncol = 3, byrow = T)
c <- eigen(b) # 求b的特征值与特征向量

线性模型

1.变量之间的关系一般分为两类

• 完全确定的关系，即可表达为函数解析式
• 非确定的关系，也称相关关系

2.回归分析研究的主要内容

• 通过观察或实验数据的处理，找出变量间相关系数的定量数学表达式—经验公式，即进行参数估计，并确定经验回归方程的具体形式

• 检验所建立的经验回归方程是否合理

• 利用合理的回归方程对随机变量Y进行预测和控制。